Виды и источники неопределенностей. Виды возмущений. Основные классы адаптивных систем. Отличие поисковых и беспоисковых систем с самонастройкой. Особенности прямого и непрямого адаптивных подходов, страница 5

Система с явной эталонной моделью по способу достижения цели упр-я можно разделить на системы с параметрической и сигнальной адаптацией. В системах с сигнальной настройкой эффект адаптации достигается без изменения параметров управляющего воздействия за счёт повышения коэффициента усиления или на основе создания скользящих режимов. При этом к управляющему воздействию добавляют специальный сигнал – сигнал адаптации.

В системах с парам-ой адаптацией цель упр-я достигается за счёт изменения параметров управляющего устройства. Такие сис-мы более универсальные, но имеют более сложную структуру. Сложность таких систем определяется числом настраиваемых параметров.

С целью повышения точности системы и быстродействия процесса адаптации применяются алгоритмы, сочетающие в себе методы сигнальной и парам-ой адаптации. Параметрическая часть настройки служит для стабилизации коэффициента усиления в требуемых пределах.

В случае сигнальной адаптации происходит подстройка к аддитивным. Мат. модель для сис-мы с сигнальной адаптацией, синтезированной методом вектора скорости:

Уравнение ОУ:

Закон управления: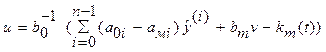

где k_m(t)  настраивается по алгоритму: ,где γ_m -коэффициент передачи адаптера, l_m – вспомогательная функция. С помощью γ_m и l_m достигается поставленная цель управления, т.е. значения γ_m и l_m  определяются из условия устойчивости адаптивной системы.  При параметрической адаптации происходит постройка к параметрическим возмущениям (при отсутствии аддитивных возмущений). Математическая модель для системы с параметрической адаптацией, синтезированной методом вектора скорости:

Уравнение ОУ:  

Закон управления:    

Пусть коэффициенты регулятора образуют вектор настраиваемых коэффициентов θ^Т = (k_i(t) , k_b), тогда алгоритм адаптации на основе метода вектора скорости запишется в виде  или для повышения быстродействия адаптора можно использовать алгоритм настройки следующего вида: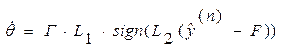         

где Г– матрица коэффициентов передачи, Г=diag{γ_j}; L–диагональная  вектор-функции. Значения элементов матриц Г и L опр-ся из условия устойчивости адаптивной системы.

При сигнально – параметрической адаптации присутствуют и аддитивное и парам-ое возмущения. Мат. модель  сис-мы, синтезированной методом вектора скорости:

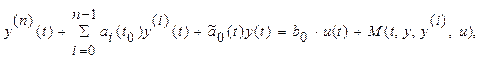
   ,     изменение которых подчиняются алгоритмам:               

9)       Понятие обобщенного настраиваемого объекта, основного контура. Методы синтеза алгоритмов основного контура.

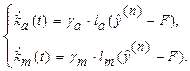
Т.к. адаптивные системы управления отличаются от традиционных (неадаптивных) систем управления наличием контура адаптации, то для формулировки задачи синтеза алгоритма адаптации удобно использовать понятие «обобщённого настраиваемого объекта» (ОНО). ОНО включает в себя всю неизменяемую часть системы (объект, регулятор основного контура и устройства преобразования (датчики)). В качестве входа ОНО могут выступать как настраиваемые параметры регулятора, так и входы обобщённого объекта, если основной контур управления отсутствует. Основной контур адаптивной системы – это контур управления. Цепь обратной связи, включающая адаптор, называется контуром адаптации.

Полагаем, что модель ОУ описывается уравнением:

= f(t, x, y, u, q)

y = g (t, x, u, q), q Î R^r – вектор параметрических возмущений, x Î Rⁿ , y Î R^l, u Î R^m

q_min £ ½q½£ q_max; q Î W_q , t₀ £ t £ t_k

Цель функционирования системы, как правило, задаётся с помощью предельного выражения: lim Q £  d, t₀ £ t £ t_k

Q – скалярная функция качества (целевая функция)

d - допустимое значение (min) для целевой функции Q, d ³ 0

Задача синтеза адаптивной системы управления: определить вид управляющего воздействия u = u(x,y,k)

(k – вектор настраиваемых коэффициентов) и алгоритм изменения настраиваемых коэффициентов k = k(x,y,r) (r – вектор эталонных входных сигналов), чтобы для возмущений из класса W_q выполнялась поставленная цель управления.

Этапы синтеза адаптивных систем :

1.  Определение уравнения основного контура

2.  Синтез алгоритма адаптации (алгоритма настройки коэф-тов регулятора)

Методы синтеза основного контура