Виды и источники неопределенностей. Виды возмущений. Основные классы адаптивных систем. Отличие поисковых и беспоисковых систем с самонастройкой. Особенности прямого и непрямого адаптивных подходов, страница 9

(аргументы вектор-функции опущены  для упрощения записи выражений),

  Г_i^T = Г_i > 0 – квадратная матрица коэффициентов (i = 1, 2), Г₂ – диагональная матрица, sign (.) – вектор состоящий из знаков компонент вектора Ñ_q w .

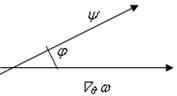     - 90⁰ ≤ j ≤ 90⁰                Рисунок 3.5

АСГ вида (3.22) называют алгоритмом в конечно-дифференциальной форме. Частными случаями (3.22) являются алгоритмы в дифференциальной форме (при y = 0)

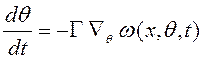                                        (3.23)

и в конечной форме (для Г = 0)                                                (3.24)

где g - шаг дискретизации.

В вопросе 16 описан сам синтез  алгоритмов адаптации методом скоростного градиента.

16)Последовательность синтеза адапивных систем на основе АСГ.

Рассмотрим пример синтеза системы  с параметрической адаптацией.  Сформулируем задачу синтеза для объекта управления, который задан моделью в пространстве состояний     (3.25) Эталонная модель (3.26)   где rÎR^m– задающее воздействие, А_м – гурвицева матрица. Цель управления сформулирована относительно координатного рассогласования        (3.27)    где e(t)=x(t)–x_м(t). Предполагаем выполнение условия управляемости и наблюдаемости координат состояния. Пусть целевой функционал выбран в форме скалярной квадратичной функции          (3.28) Поставленная цель управления выполняется, если Q®0  при  t®¥.

Синтез адаптивного регулятора начнем с определения уравнения основного контура.    Уравнение основного контура можно получить модальным методом, т.е. разрешив уравнениеотносительно u (t):

или       (3.29)  “Идеальное” управление можно записать в форме       (3.30) где матрицы k_*^x, k_*^r удовлетворяют условию                                                               .               (3.31)

Матрицы идеальных значений коэффициентов регулятора k_*^x, k_*^r существуют, если выполняются ранговые условия  

Реальный закон управления имеет вид    (3.32) где k^x (t), k^r (t) – матрицы настраиваемых коэффициентов регулятора, 

Для определения вида алгоритма адаптации требуется вычислить производную целевого функционала, т.е.              (3.33)

После подстановки (3.32) в (3.33) имеем      (3.34)

Определим скоростные градиенты

Для алгоритмов настройки коэффициентов выбираем АСГ в дифференциальной форме  (3.35)      где Г = gI,  g > 0 .

   Система (3.25), (3.26), (3.32), (3.35) относится к системам с параметрической адаптацией. На основе АСГ можно синтезировать также системы с сигнальной и сигнально-параметрической адаптацией.

Системы с алгоритмом адаптации (3.35) сохраняют работоспособность при изменении координатных и параметрических возмущений в широких пределах.  Качество процессов ухудшается, если скорость изменения параметрических возмущений высокая.

17)     Основные этапы синтеза адаптивных алгоритмов управления вторым методом Ляпунова.

Второй метод Ляпунова был разработан для исследования устойчивости движения нелинейных систем, которые описываются обыкновенными дифференциальными уравнениями. V – функция Ляпунова (скалярная). Если система устойчива, то V всегда имеет свойства: à  система асимптотически устойчива.

объекта управления     (3.25) Желаемая динамика задаётся эталонной моделью вида (3.26)       Цель функционирования системы задана предельным уравнением (3.27)        где e– ошибка системы.

 Синтез основного контура ОУ (3.25) подвержен действию парам-ких возмущений. Для получения «идеального» рег-ра запишем уравнение в отклонениях     (3.43)

Условие разрешимости согласно (3.43) имеет вид    (3.44) Разрешая (3.44) относительно u(t), имеем   домножим слева на B^T          полагаем det (B^TB) ¹ 0 , тогда умножим на  (B^TB)^-1 , имеем    .       (3.45)   Если реализовать управление вида (3.45), то система будет описываться уравнением   Решение этого уравнения равномерно асимптотически устойчиво в силу гурвицевости матрицы А_м. Следовательно, при «идеальном» законе управления (3.45) цель достигается.

Уравнение идеального закона управления (3.45) запишем в виде    (3.46)

где  - матрицы идеальных коэффициентов регулятора. Приравнивая коэф-ты в (3.45), (3.46),  найдём соотношение между ними, при х:             (3.47) при r:        (3.48)                  подставив (3.48) в (3.47), имеем .          (3.49)