 Cистемой
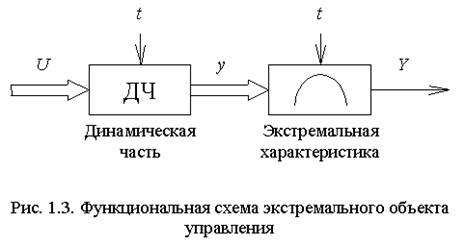
экстремального регулирования называют СУ в которой на ряду с динамической
частью имеется статический показатель качества работы, который необходимо
поддерживать на мин./макс. уровне. Количество
экстремумов, их положение, и аналитическое выражение функции качества в общем
случае может быть не известны. Показатель качества с течением времени может
меняться под воздействием окр. среды (дрейф). Регулятор должен обеспечивать
определение экстремума и стабилизацию СУ в найденной точке.
Cистемой
экстремального регулирования называют СУ в которой на ряду с динамической
частью имеется статический показатель качества работы, который необходимо
поддерживать на мин./макс. уровне. Количество
экстремумов, их положение, и аналитическое выражение функции качества в общем
случае может быть не известны. Показатель качества с течением времени может
меняться под воздействием окр. среды (дрейф). Регулятор должен обеспечивать
определение экстремума и стабилизацию СУ в найденной точке.
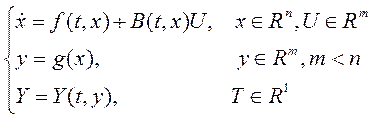 Математическая
модель объекта:
Математическая
модель объекта:
x - вектор состояния
объекта; y- вектор выходных
переменных ДЧ объекта; Y(y,t)- выходная переменная экстремального
объекта, которая представляет собой нелинейную однозначную функцию и имеет экстремум
по переменной y; Зависимость f и B от t отражает
влияние действующих на объект возмущений, зависимость Y от t отражает
дрейф экстремума во времени. Предполагается, что параметры динамической части
объекта f(x,t) и B(x,t) могут изменяться в
заранее указанных пределах (![]() ). Темп изменения Y, f и B на порядок медленнее
основных процессов в объекте. Задача синтеза экстремальной системы: необходимо
рассчитать регулятор, т.о. чтобы в замкнутой системе выполнялось условие: Extr Y(t,y)=Y0 где Y0 - экстремальное
значение выходной характеристики. Могут предъявляться требования к процессу
поиска экстремума:
). Темп изменения Y, f и B на порядок медленнее
основных процессов в объекте. Задача синтеза экстремальной системы: необходимо
рассчитать регулятор, т.о. чтобы в замкнутой системе выполнялось условие: Extr Y(t,y)=Y0 где Y0 - экстремальное
значение выходной характеристики. Могут предъявляться требования к процессу
поиска экстремума: ![]() . Т. к. Y0 соответствует
определенное значение y0, задачу синтеза можно переформулировать. Для
экстремального объекта необходимо рассчитать регулятор, кот. обеспечит
выполнение свойства lim y(t)=y0 при t->∞ для вых.
переменной ДЧ.(условие системы стабилизации) с требуемыми показателями *.
. Т. к. Y0 соответствует
определенное значение y0, задачу синтеза можно переформулировать. Для
экстремального объекта необходимо рассчитать регулятор, кот. обеспечит
выполнение свойства lim y(t)=y0 при t->∞ для вых.
переменной ДЧ.(условие системы стабилизации) с требуемыми показателями *.
При синтезе экстремальных систем можно выделить 3 задачи:
1)задача оценки градиента; 2)организация движения системы экстремуму G®0; 3)стабилизация системы в точке экстремума при наличии дрейфа.
где 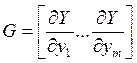 -
градиент (вектор частных производных).
-
градиент (вектор частных производных).
Возможны различные варианты описания характеристики Y(t,y) для одноканального объекта:
1) Экстремальная характеристика типа "модуль"
при отсутствии дрейфа: Y=½y½.
В общем случае : Y=k(t)|y-y0(t)|+Y0, (дрейф есть)
|
|
y0(t)-отражает горизонтальный дрейф экстремума, Y0(t) - вертикальный дрейф k(t) –смешанный дрейф( искажение формы ЭХ). |
2) ЭХ типа "парабола"
|
|
При отсутствии дрейфа: Y=y2 . В общем случае : Y=k(t)(y-y0(t))2+Y0 |
3) Парабола произвольного n-го порядка
Y =kn(t)|y-y0(t)|n +…+k1(t) |y-y0(t)|+Y0(t) при наличии дрейфа.
4)
Многоканальный объект Матричное описание ЭХ (квадратичная форма) Y=yTВ(t)y (без дрейфа.) В
общем случае ![]()
Зависимость элементов матрицы В(t) отражает изменение во времени экстремальной характеристики.
(Способ деления производных)
Для одноканальных объектов, статическая экстремальная характеристика которых имеет вид Y=Y(y,t), y € R1
Определим полную производную выходной переменной по времени
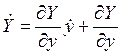
Второе слагаемое в выражении обусловлено наличием дрейфа.
При медленном дрейфе экстремальной характеристики им можно пренебречь, так как ![]() . В этом случае можно определить величину
градиента как отношение двух полных производных по времени: G =
. В этом случае можно определить величину
градиента как отношение двух полных производных по времени: G =![]() (1)
(1)
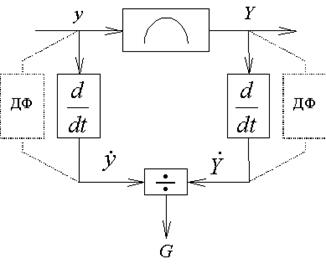
Рис. 1 Структурная схема устройства оценки градиента методом деления производных
Поскольку операция идеального дифференцирования на практике нереализуема, для оценки производных следует использовать дифференцирующие фильтры (показаны пунктиром).
Достоинство данного способа: простота технической реализации.
Недостатки 1) необх. Точно оценить производные
(дифференцирование усиливает помехи). Для уменьшения влияния помехи вместо
идеальных дифференцирующих устройств нужно использовать дифференцирующие
фильтры выше первого порядка с малыми постоянными времени.2) невозможно оценить
градиент при малых значениях ![]() и =0. Поэтому
невозможно применить на практике.
и =0. Поэтому
невозможно применить на практике.
Данный метод оценки градиента применяется для одноканальных
объектов со статической экстремальной характеристикой Y=Y(y,t), y
€ R1. Здесь, производные ![]() и
и ![]() представляются в виде конечных разностей
представляются в виде конечных разностей
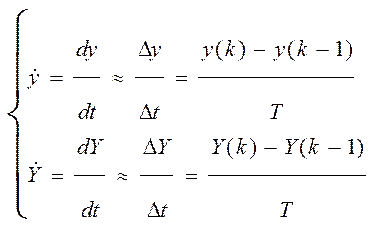
,где k - дискретный момент времени; T - шаг квантования (дискретизации).
В основе способа лежит приближенное соотношение:
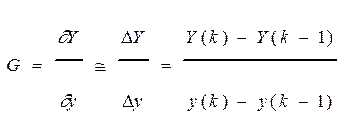
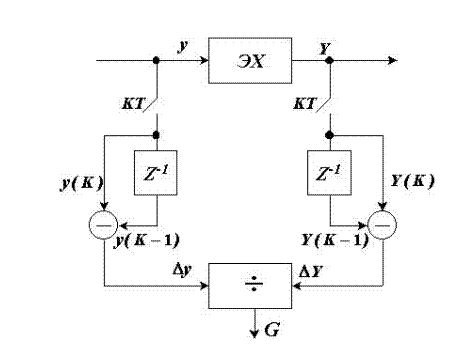
Рис. 1. Структурная схема оценки градиента методом конечных разностей
Достоинство данного метода в высокой помехозащищенности, так как дифференцирование отсутствует.
Недостатком метода является невозможность оценки при малых приращениях Δy и Δy =0.
Оценка знака градиента 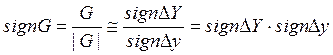
Способ синхронного детектирования предполагает добавление к основному сигналу на входе экстремальной характеристики y дополнительного поискового синусоидального сигнала малой амплитуды и высокой частоты Δy=Asinωt с последующим выделением соответствующей составляющей из выходного сигнала Y.
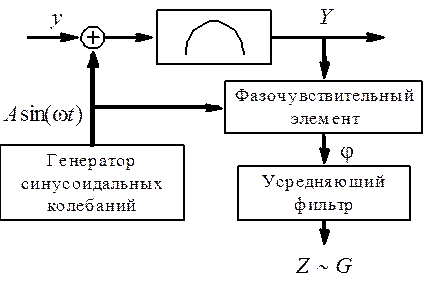 В зависимости от разности фаз делается вывод
о знаке G.
В зависимости от разности фаз делается вывод
о знаке G.
Для получения величины G в систему добавляют усредняющий фильтр. Работу метода синхронного детектирования иллюстрирует график рис.2.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.