|
|
1 – ограничения
накладываются на переменные состояния объекта x € ΩX |
2) Ограничение на управление
u € ΩU
Rm . | uj | ≤ u j max , j = 1…m
Начальные и конечные состояния
|
|
|
|
1 – задача с фиксированными концами |
2 – задача с подвижным правым концом. |
|
|
|
|
3 – задача с подвижным левым концом |
4 – задача с двумя подвижными концами |
3) Критерий
оптимальности. Требования к процессу перехода из нач-го состояния в конечное
задаётся в виде некот-го обобщённого показателя качества, кот наз-ся критерием
оптим-ти.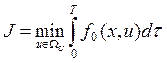 
( минимум по управлению)
Т – длительность процесса. В зависимости от требований к качеству работы системы м выделить несколько наиболее часто встречающихся критериев оптим-ти:
|
1) Критерий быстродействия |
J = |
|
2) минимум затрат энергии по состоянию |
J = J = |
|
3) минимум затрат энергии на управление |
J = |
4) Форма результата.
1. U 0 = U 0 (t) – программное управление (для систем работающих в режиме вкл/выкл ).
2 . U 0 = U 0 (x) –управление в виде обратной связи (при наличии внешних возмущений).
Основные соотношения метода. Общий класс ОУ:
= f (x , u), x € Rn , u € Rm , m ≤ n. Переменные сост-я
(| xi | ≤ 
, i = 1….n) и ресурс упр. (| uj | ≤ u j max , j = 1…m) огранич-ы.
Нужно опред-ть управляющее воздействие, кот обеспечивало бы переход из нач-го состояния x(t) в конечное x(T) за время Т в соответствии с критерием оптимальности
|
J = |
|
Выберем на оптимальной траектории перехода промежуточную точку x(t + Δt), расположенную достаточно близко к заданной нач. точке. По принципу оптим-ти конечный участок есть также оптимальная траектория, поэтому представим критерий оптим-ти в виде суммы двух критериев, соответствующих двум участкам движения,
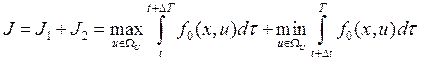
(f0(x,u)+(∂V/∂xT)*
)=0. Вместо 
подставим
правую часть объекта
( f 0 ( x, u) + (∂V / ∂ xT )* f (x , u)) = 0 (**)
Т о, оптимальным б. управление, кот минимизирует выр-е (**). Но исполь-ть его для вычисления U0 нельзя, т к одно ур-е содержит m+1 неизвестных ( U0 € Rm и V € R1 ).
Расчётные соотношения метода
В случае оптим-го управления u = u0 соотношение (**) принимает вид
f 0 ( x, u0 ) + (∂V / ∂ xT )* f (x , u0 )) = 0 (***)
Продифференцируем по uвдоль оптимальной траектории
∂ f 0 ( x, u0 ) / ∂ u | U=U0 + (∂V / ∂ xT )* ∂ f (x , u0 ) / ∂ u | U=U0=0 (****). Добавив (****) к (***) получим систему из m+1 уравнений с m+1 неизвестными, решая кот м найти оптимальное управление. Т к эти уравнения представляют собой ур-я в частных производных, для опред-я из них оптим-го управления, как пр-ло, приходится исп-ть приближ численные методы. В рез-те найденное управление получается не оптимальным, а близким к нему.
Задача отыскания точного оптимального управления методом динамического программирования носит наз-е задачи АКОР (аналитического конструирования оптимальных регуляторов). Эта задача имеет решение при следующих условиях:
1)
Объект
управления описывается линейным уравнением состояния =
A x + Bu , x € Rn , U0 € Rm , m ≤ n
2) Переход из нач точки x(0) в конечную x(T) рассматривается на бесконечном интервале времени (Т → ∞).
3) Критерий оптимальности имеет вид квадратичной формы
J =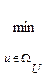 
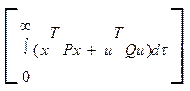
Оптимальное управление, полученное методом динамического программирования, для такой постановки задачи б иметь вид u0 = Kx . Т о, оптимальным управление для задачи АКОР будет пропорциональный з-н управления.
(метод расчёта оптимального управления). Запишем основные соотношения принципа максимума на основе уравнений метода динамического программирования. Основное соотношение:
( f 0 ( x, u) + (∂V / ∂ xT )* f (x , u)) = 0 (*)
Т к мин. ф-ии равен макс. этой же функции с противоположным знаком , то запишем:
( - f 0 ( x, u) - (∂V / ∂ xT )* f (x , u)) = 0 (**)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
p I X I 2
dτ p I - весовой коэф-т