Формулировка задачи синтеза экстремальных систем. Описание экстремальных характеристик. Простейшая непрерывная оценка частной производной. Дискретная оценка частной производной (метод деления конечных разностей). Оценка градиента способом синхронного детектирования. Оценка градиента при помощи специального фильтра. Шаговые экстремальные системы, страница 3

, которое представляет собой нелинейное дифференциальное уравнение относ. переменной y. Полагая , запишем для него Ур-е статики kG(y,t) = 0, (***), где завис-ть G от t параметрич-я.Поскольку k≠0,из выраж-я (***) следует G(y,t)=0(****)

Таким образом, в случае устойчивости замкнутой системы процессы в ней будут сходиться к точке равновесия, которая является точкой экстремума. Устойчивость движения в замкнутой системе можно обеспечить соответствующим выбором коэффициента усиления k, при этом выход на экстремум происходит автоматически.

9. Метод “тяжелого” шарика

Данный метод позволяет организовать движение к глобальному экстремуму в случае, когда ЭХ имеет локальные экстремумы. СУ проскакивает локальные экстремумы, благодаря введению доп. инерционности для придания процессам колебательного характера. При этом для объекта 1-го порядка, замкнутая система имеет вид:

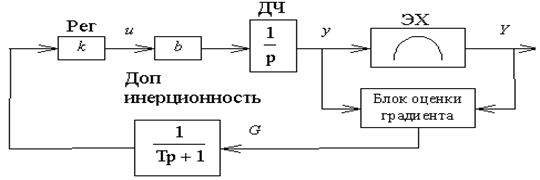Операторное уравнение замкнутой системы:

y = b*k *G/ [p(Tp+1)] (*)

где 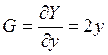, так как экстремальная характеристика описывается уравнением Y=y².

Преобразуем уравнение (*) к виду: p(Tp+1)y=2bky, которое представим в стандартной форме: (Tp² +p-2bk)y=0. Таким образом, точка равновесия y⁰ =0 эквивалентна точке экстремума, G=0. Характер движения системы к точке экстремума определяется характеристическим уравнением Tp² +p-2bk = 0.

Выбирая распределение корней из условия обеспечения требуемых показателей качества процесса выхода на экстремум (t₀^* и σ ^* % ≠ 0), сформируем желаемое характеристическое уравнение второго порядка. Приравнивая коэффициенты при соответствующих степенях оператора pэтих двух уравнений(согласно методике модального метода синтеза), определим численные значения kи T ( таким образом, чтобы процесс в системе был колебательным и обладал заданной длительностью и s.

10. Одноконтурные системы со старшей производной в управлении

На ряду с условием статики lim y(t)=y0 при t->∞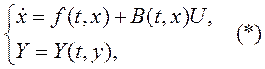, предъявляются условия к динамике (tп*,σ*,Δ*)

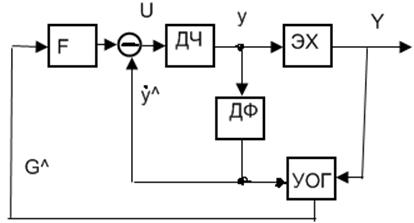В случае идеального дифференцирования поведение замкнутой системы описывается уравнением: , в статике имеем y=y0(G=0). Движение в этом случае обладает особенностями: процесс монотонный, соотв. требования по быстр, не имеет колебаний вокруг экстр. При реализации зу U=k[F(.)-y^(.)] необходимо предусмотреть возможность измерения y^(.)(t) и G. Для оценки производной можно использовать ДФ, а для градиента спец фильтр, поскольку уже оценивается y^(.)(t) .

Для получения адекватных оценок производных, ДФ и УОГ должны обладать малыми инерционностями. Поскольку для оценки G испол оценка y^(.)(t) , то .

Вследствие этого в системе возникают разнотемповые движения: 1. -сверхбыстрые, 2. -быстрые, 3. медленные – основные, соотв процессу движения к экстремуму.

Поиск экстр осущ к не нулевому нач сост y(0)/=0. Для того, чтобы процесс поиска соотв предъявл к нему требованиям должны быть согл:

11. Двухконтурные системы со старшей производной в управлении

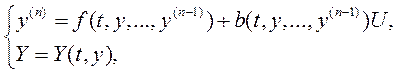
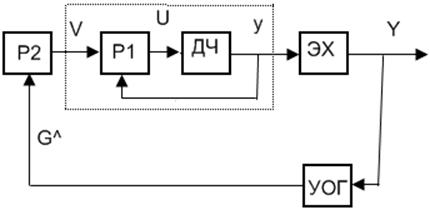Используется метод старшей производной с учетом особенностей ЭО. Учтем особенности объекта, предварительно стабилизировав динамическую часть, а затем организуем движение к этому режиму. Синтезируем двухконтурную систему

Необходимо разнести процессы стабилизации и поиска экстремума, при расчете регуляторов будем ориентирована на требование tп1<<tп2.

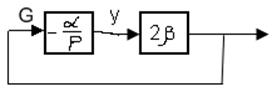
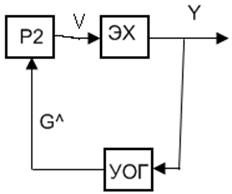
Получаем 2 этапа: 1. Стабилизация ДЧ(по окончанию переходного процесса этот контур вырождается в единый контур усиления) ; 2. В качестве Р2 выбирается интегратор 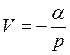 и ->, получаем эквивалентную струк схему:

Коэф. находится модальным методом на основе требований к быстродействию tп1. Подход действует для медленных процессов.

12. Постановка задачи синтеза оптимальных систем

Оптимальными СУ называютт системы, в кот-х максимально использованы возможности объекта при совершении переходных процессов в рамках существующих ограничений.

1) Описание объекта. Описание представлено в переменных сост.:

; О. д.б. стационарным f(x,u) – вектор нелин-х фунций, удовлет-щих условию существования и единственности реш-я диф уравнения. В частном случае объект м б описан нелинейным стационарным уравнением:

,где В – матрица нелинейных функций.

- линейный стационарный объект.

1) Ограничения на объект.