Формулировка задачи синтеза экстремальных систем. Описание экстремальных характеристик. Простейшая непрерывная оценка частной производной. Дискретная оценка частной производной (метод деления конечных разностей). Оценка градиента способом синхронного детектирования. Оценка градиента при помощи специального фильтра. Шаговые экстремальные системы, страница 5

Преобразуем (**), введя ряд обозначений:

Z =	1) введём вектор сопряжённых координат Z – представляет собой вектор состояния объекта, дополненный нулевой координатой. Z € R n+1
	1) введём расширенный вектор правых частей φ € R n+1 2) вектор сопряж-х корд-т (специфический) Ψ € R n+1 Ψ = [ -1  -∂V/∂x1   ….  -∂V / ∂xn]

Определим скалярное произведение H = Ψ (z) φ (z,u), кот-й наз-ся гамильтонианом.  

H = - f₀ (x,u) - ∂V/∂x ^T * f (x,u).

Основное соотношение метода: H( z,u ) = 0. Управление из области допустимых значений, кот-е обеспечивает максимум гамильтониана яв-ся оптимальным. По сути переходим к задаче поиска экстремума. Необходимое условие экстремума: ∂H/∂u^T = 0. Найденное из этого условия, управление может выходить за пределы допустимых значений (при  ограниченном ресурсе, например | u | ≤ U_max). Поэтому в качестве оптимального управления берутся предельные значения управления, лежащие на границе обл-ти допустимых значений ( U_max).

Процедура синтеза регулятора

1) описание объекта приводится к стандартному виду (в переменных состояния) =f(x,u) записывается критерий оптимальности.

2) Вводятся расширенный вектор состояния Z, вектор правых частей φ и сопряжённых координат Ψ.

3) Формируется гамильтониан в виде скалярного произ-я ф-ций: H = Ψ (z) φ (z,u)

4) Из условия максимума гамильтониана опред-ся оптимальное управление как фун-я сопряж-х координат Н : u ⁰ = u⁰ (Ψ)

5) Формир-ся система диф уравнений для нахождения сопряжённых координат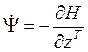

6) Вычисляется оптим-ное управление в виде ф-ции времени (программное управление) u⁰ = u⁰ (t)

7) Различными способами пытаются перейти от программного управ-я к управлению в виде обратной связи u⁰ = u⁰ (x)

16.  Процедура синтеза оптимальных систем на основе принципа максимума Понтрягина

Процедура синтеза регулятора

1) Ставится задача синтеза и описание объекта приводится к стандартному виду (в переменных состояния) =f(x,u)

2) Вводятся расширенный вектор состояния Z, вектор правых частей φ и сопряжённых координат Ψ.

3) Определяется гамильтониан в виде скалярного произ-я ф-ций: H = Ψ (z) φ (z,u), при этом используется частная производная по U, либо подставляется максимальное значение.

4) Из условия максимума гамильтониана опред-ся оптимальное управление как фун-я сопряж-х координат Н : u ⁰ = u⁰ (Ψ)

5) Формир-ся система диф уравнений для нахождения сопряжённых координат

6) Вычисляется оптим-ное управление в виде ф-ции времени (программное управление) u⁰ = u⁰ (t)

7) Различными способами пытаются перейти от программного управ-я к управлению в виде обратной связи u⁰ = u⁰ (x)

17. Особенности задачи оптимального быстродействия

а) Рассмотрим общий класс объектов управления (Гамильтониан быстродействия)

 с ограниченным управлением u € Ω_U(чаще всего u_i≤|u_im|) и критерием оптимальности J = 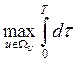. Сформируем гамильтониан согласно процедуре синтеза на основе принципа максимума

H = -1 +  Ψ₁ *f₁ (.)+ … + Ψ_n * f_n (.). его макс. =0.

В задаче оптимального быстродействия 1-ое слагаемое гамильтониана константа, не зависит от управляющего воздействия, а следовательно, не влияет на максимум гамильтониана по U. Поэтому, с целью упрощения в задаче оптимального быстродействия нет необходимости расширять вектор состояния объекта. Для неё формируется, так называемый, гамильтониан быстродействия H_б = (x) f (x,u). В этом случае уравнение принципа максимума принимает вид H_б = 1 u ⁰ = u⁰ (t)

б) Для объектов с аддитивным управлением (разрывное управление)

формируем гамильтониан быстродействия

H_б = ( Ψ₁ *f₁ (.)+ … + Ψ_n * f_n (.)) + (Ψ₁ *B₁ (.)u+ … + Ψ_n *B_n(.)u).

Управление всегда носит релейный характер:

U⁰ = U_m*sign (ΨB)

в) для класса линейных объектов (теорема о числе переключений)

Т.к. управление входит аддитивно, то оптим-ное  управление носит релейный характер.

Теорема о числе переключений. Если корни характеристического уравнения вещественные, то число переключений управляющего воздействия не превышает (n-1), где n – порядок объекта. Эта теорема справедлива как для устойчивых, так и для неустойчивых объектов.

Пример: n = 3

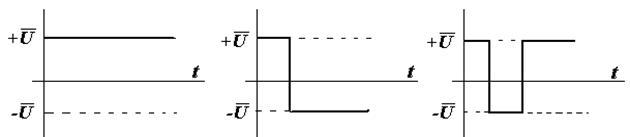
1-  нет переключений, 2 – одно перекл., 3 – 2 переключ.