Формулировка задачи синтеза экстремальных систем. Описание экстремальных характеристик. Простейшая непрерывная оценка частной производной. Дискретная оценка частной производной (метод деления конечных разностей). Оценка градиента способом синхронного детектирования. Оценка градиента при помощи специального фильтра. Шаговые экстремальные системы, страница 2

Наличие колебаний на входе приводит к появлению колебаний такой же частоты на выходе, причем при прохождении экстремума колебания на выходе изменяют фазу на 180⁰. если - не достигли экстремума.

Для сравнения сигналов с входа и выхода экстремального объекта используется специальное фазочувствительное устройство. Если -разность фаз, то на выходе фазочувствительного устройства -положительный сигнал, в противном случае – отрицательный. Этот сигнал, пройдя через специальный фильтр, будет пропорционален частной производной

В качестве фазочувствительного элемента можно использовать блок умножения.

При малой амплитуде поискового сигнала можно считать, что статическая экстремальная характеристика линейна. На выходе фильтра получим сигнал, пропорциональный градиенту z=π A² G.

Метод синхронного детектирования позволяет получить оценку G, пригодную для формирования движения к экстремуму, хорошо защищен от помех и часто применяется. Может применяться для многоканального варианта ДЧ. В этом случае используются несколько ГСК различных по w по 1 на каждый канал, полосовые фильтры на выходе.

Недостаток: наличие колебаний на выходе. В точке экстремума возникают автоколебания. Их w зависит от w поисковых колебаний.

6. Оценка градиента при помощи специального фильтра

Данная схема – неявная реализация способа деления производных, где вместо операции деления - умножение.

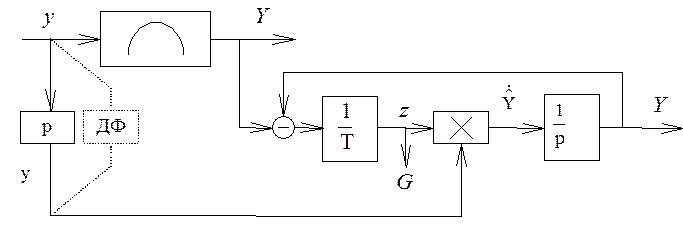
Промежуточная переменная z определяется соотношением

  (*), где - оценка выходной переменной экстремального объекта; T - постоянная времени устройства.

Запишем уравнение динамики фильтра оценки градиента относительно переменной z , для чего продифференцируем по времени соотношение (*):(**) преобразуем 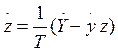. Учитывая, что , представим (**) в виде: . При достаточно малом значении постоянной времени (Т→0) уравнение вырождается в соотношение: ,или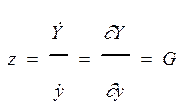

На практике необходимую для оценки градиента производную  оценивают с помощью дифференцирующего фильтра (показан пунктиром), имеющего малую постоянную времени. Точность метода тем выше, чем Т меньше.

Постоянная времени ДФ д.б. меньше на порядок постоянной времени ФОЧП. В этом случае при реализации системы экстремального регулирования в ней будут возникать 3 вида разнотемповых процессов, что не удобно на практике. С целью упрощения реализации ДФ в ряде случаев постоянные времени м выбирать соизмеримыми (загрубляют G).

7. Шаговые экстремальные системы

Основаны на пошаговом сравнении выхода экстремального объекта. Применяются для объекта с малоинерционной ДЧ. Дискретные САУ.

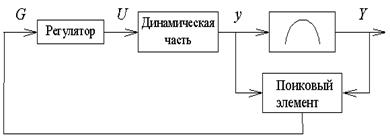Вид экстремума известен заранее (мин./макс.).

В нач момент времени делается пробные шаги влево и вправо и определяется соответ-щее значение функции качества:  y_* ± Δy → Y(y_* ± Δy) = Y1. И сравниваются между собой.

Если при поиске максимума значение больше первоначального значения, делается следующий шаг в том же направлении до тех пор, пока не проскочим т. экстремума, когда значение показателя качества может оказаться меньше предыдущего, при этом направление меняется. В результате вокруг точки экстремума возникают незатухающие колебания, их величина зависит от величины шагов.

Y(y₀ + Δy) > Y₀ , Y(y₀ - Δy) > Y₀ →Y₀ – min

Y(y₀ + Δy) < Y₀ , Y(y₀ - Δy) < Y₀ →Y₀ – max

Недостатки: 1) невозможно обеспечить заданное качество процесса движения к экстремуму. 2) наличие колебаний приводит к доп. затратам энергии. Иногда используют переменный шаг, который уменьшается по мере приближения к экстремуму, при этом время выхода на экстремум увеличивается.

8. Градиентные системы первого порядка

В качестве основных способов  организации движ-я к экстр. м. выделить 2 подхода: 1) шаговые системы  и системы с запоминанием экстр., с косвенной оценкой движения к экстремуму (без определения градиента); 2) градиентные экстремальные системы.

Градиентные системы 1-го порядка Рассмотрим организацию движ-я к экстремуму на примере простейшего объекта упр-я, кот-й описывается следующей сис-мой уравнений:

 (*)

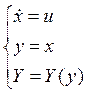Сформируем пропорциональный градиенту закон управления в виде u=kG(y,t) (**).Подставив (**) в уравнение объекта (*), получим уравнение замкнутой системы