Формулировка задачи синтеза экстремальных систем. Описание экстремальных характеристик. Простейшая непрерывная оценка частной производной. Дискретная оценка частной производной (метод деления конечных разностей). Оценка градиента способом синхронного детектирования. Оценка градиента при помощи специального фильтра. Шаговые экстремальные системы, страница 6

При наличии комплексно-сопряжённых собственных значений матрицы А, число переключений в системе м б произвольным. В асимптотике оно стремится к ∞, в реальных системах с учётом реализации релейного элемента, как правило, 10-15.

18.  Метод поверхности переключения

Применяется для формирования опт. управления в виде обратной связи, в случае когда управление разрывно (релейный характер).

. Переход из начальных состояний в заданные конечные в соответствии с критерием оптимальности: J = .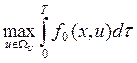

Оптимальный з-н управления в этом случае имеет вид:

S(x) – вектор функций, определяющих в пространстве состояний некоторую поверхность, которая наз-ся поверхностью переключения. .

Для определения этой поверхности конечная точка  «приводится» к началу координат. Затем в пространстве состояний исследуются траектории перехода из произвольных начальных состояний x (0) в конечную точку x(T) = 0.  На траекториях перехода выделяются точки, где происходит смена знака управления, которые объединяются в поверхность переключения S(x)=0.

Чтобы получить траекторию перехода из нач точки x₁ (0) в начало координат, нужно задавать нач условия для сопряжённых координат  Ψ(0). Если эти нач условия выбраны неудачно, то получим траекторию перехода не в x(T) = 0, а в произвольную точку пространства состояний. В этом случае надо снова задать новые н.у. для Ψ(0).  Объединяя точки переключения управления на всех траекториях перехода из произвольных состояний в начало координат, м получить поверхность переключения.

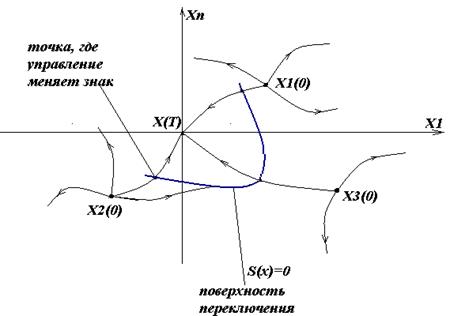
Т.о., метод поверхности переключения позволяет получить оптимальный з-н управления в виде обратной связи. .

Но при этом приходится рассматривать две совокупности нач-х условий: для переменных состояния X(0) и сопряжённых координат Ψ(0), что существенно затрудняет определение управления. Можно применять для объектов с аддитивным управлением.

19. Метод обратного времени

Этот способ позволяет в рамках метода поверхности переключения упростить поиск необходимой поверхности. Суть метода заключается в том, что начальная и конечная точки «меняются местами», что в пространстве состояний соответствует движению в обратную сторону.

+ t – обычное время : X(0) → X(T) = 0  и две совокупности нач условий: { X(0), Ψ(0)}.

- t – обратное время: X(-T) = 0 → X(0) и {Ψ(0)}.

Постановка задачи синтеза оптимальной системы в обратном времени формулируется следующим образом. Для объекта с ограниченным ресурсом управления необходимо определить оптимальное управление в виде обратной связи, которое обеспечивает переход из начальной точки X(0)=0 в конечную X(T) в соответствии с критерием оптимальности J = 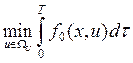. При этом заранее известно, что оптимальное управление имеет релейный характер. В этом случае нужно перебирать только одну совокупность начальных условий.

В соответствии с методом поверхности переключений в пространстве состояний на траекториях перехода выделяются точки, где происходит смена знака управления и объединяются в поверхность S(x).

20. Субоптимальные системы управления

Субоптимальными наз-ся системы, которые близки по свойствам к оптимальным с заданной точностью. Точность приближения к оптимальной системе опред-ся соотношением

В общем случае субоптимальные системы м.б. получены в резульиате:

1) аппроксимации поверхности переключений, а следовательно использование приближённого з-на управления;

2) ограничения рабочей области в пространстве состояний.

Свойства субоптимальной системы. Процессы в субоптимальной системе будут существенно зависеть от начальных условий.

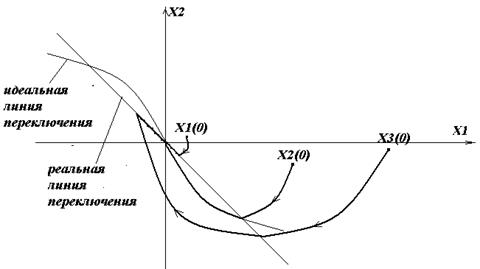
При движении из X¹ (0) изображающая точка системы попадает на реальную линию переключений  S_Р (x), а затем движется вдоль неё в скользящем режиме.

Из нач условий X² (0) – строгооптимальный процесс. Изображающая точка системы попадает в точку пересечения идеальной и реальной линий переключения и к началу координат движется по соответствующему участку идеальной линии переключений, т е по оптимальной траектории.

При движении из X³ (0) – изображающая точка б доходить до S_Р (x), переключать на траекторию, соответ-щую другому знаку управления, вновь попадать на реальную линию переключения и двиг-ся вдоль неё в скользящем режиме. Чем больше точек пересечения реал и идеал линий переключения, тем чаще в системе б возникать оптимальный процесс.