Билет№1
Задача № 1. Игральная кость бросается 1 раз. Найти вероятность следующих событий:
А1= {четное число очков}
А2= {не менее 5 очков}
А 3= {не более 5 очков}
Задача № 2. Непрерывная случайная величина Х задана своей плотностью в виде
0 при x<a и x>b
f(x)=
K(x-a) при a<x < ![]()
-K(x-b)
при ![]() <x <b
<x <b
Задача № 3. Случайный
вектор (X,Y) распределен равномерно внутри прямоугольника D={(x,y): -1![]() x
x![]() 2, 1
2, 1![]() y
y![]() 2} Описать и исследовать её и оценить P{(x,y):
-1<x
2} Описать и исследовать её и оценить P{(x,y):
-1<x![]() 0, 1
0, 1![]() y
y![]() 2}.
2}.
Решение:
Задача 1)
Ω={1,2,3,4,5,6};
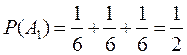
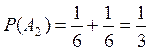
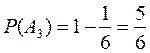
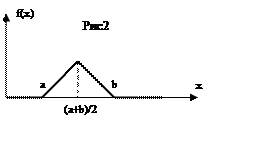
Задача 2)
tgα=K ;
Закон распределения:
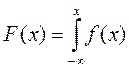 (рис2)
(рис2)
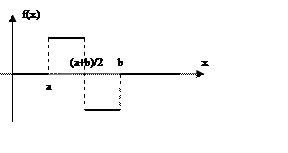
Задача 3)
![]()
![]()
 C,
xєD ;
C,
xєD ; 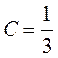 1/3,
xєD;
1/3,
xєD;
f(x,y)= 0, в др.сл. ; ; f(x)= 0, в др.сл. ;
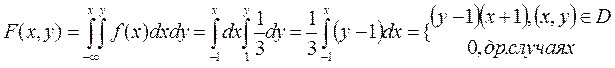
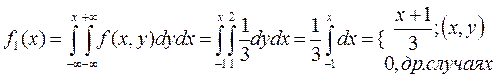
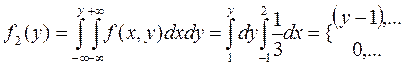 ;
; 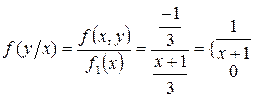
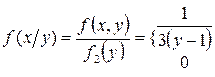 ;
; 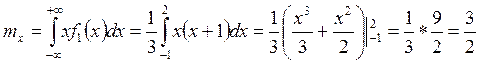 ;
; 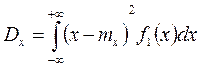 ;
; 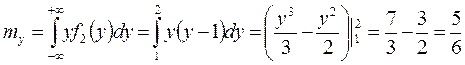 ;
; 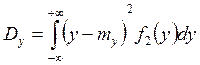 ;
; 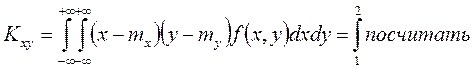
Билет№2
Задача № 1. Партия содержит N изделий, среди них n дефектных. Для контроля из такой партии выбираем r изделий. Заданны события:
A={среди отобранных равно S дефектных};
B={среди отобранных хотя бы одна дефектна};
Найти P(A) и P(B).
Задача № 2. На заводе изготавливаются однотипные изделия, причем первая линия производит 30%, вторая -35% и третья -35% всех изделий. Брак в их выпусках составляет соответственно 3%, 4% и 2%. Случайно выбирают изделия на контроль. Какова вероятность, что оно окажется достоверным?
Задача № 3. Система случайных величин (x,y) распределена с постоянной с постоянной плотностью внутри квадрата R со стороной равной 5. причем стороны составляют углы 45’ с осями координат. Необходимо описать систему (x,y), исследовать ее и построить все необходимые графики для функциональных зависимостей.
Решение:
Задача 1)
N-всего; n-дефект; r-выбираем; A – среди отобранных = S дефект; B – среди отобранных ≥ 1 дефект;
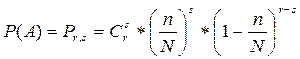 ;
; 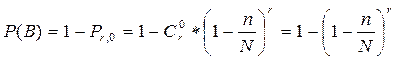
где 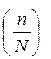 - вероятность дефекта, а
- вероятность дефекта, а 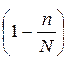 - вероятность нет дефекта.
- вероятность нет дефекта.
Задача 2)
всего 9 изделий из 100 бракованных

А={деталь стандартная}, H1={изделие с 1 линии}, H2={изделие
с 2 линии}, H3={изделие с 3 линии}. ![]()
P(A|H1) – вероятность того
что деталь стандартна при том что она принадлежит 1 линии, 97% станд. Из 30%
деталей. ![]()
![]()
![]()
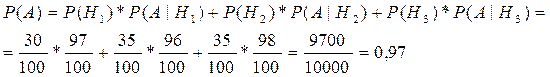
следовательно в 97% изделие окажется стандартным.
Задание 3)
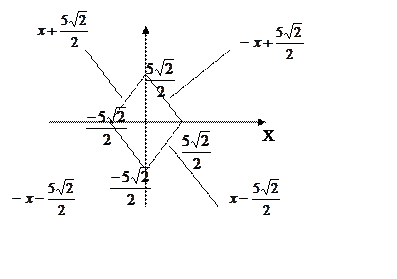
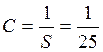
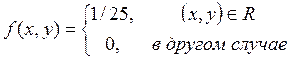
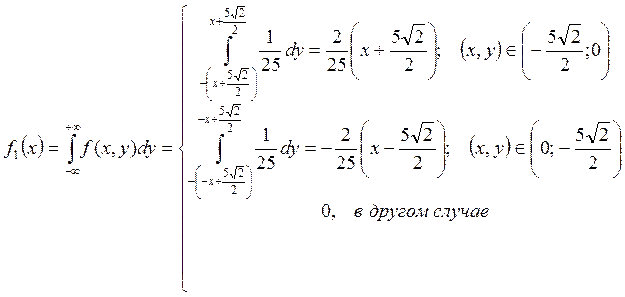
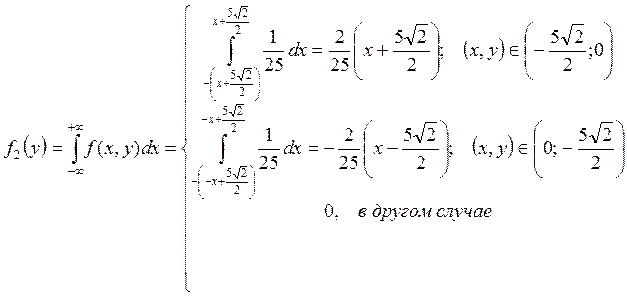
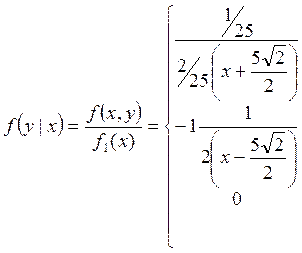
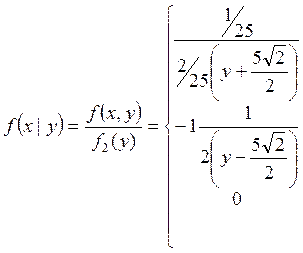
 |
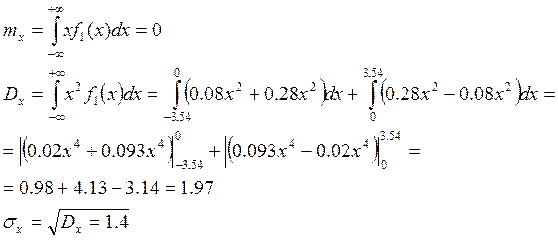
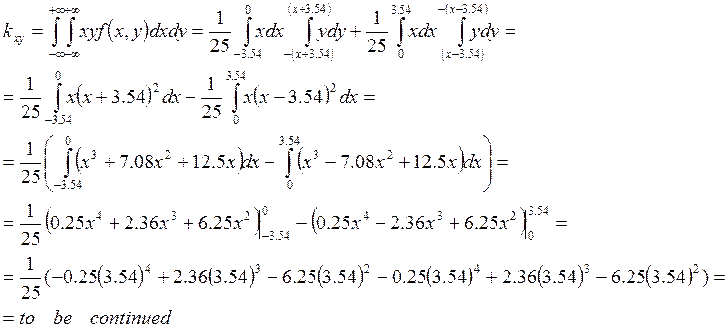
Билет № 3
Задача № 1. В урне а
белых шаров, в черных(а![]() 2,
в
2,
в![]() 3). Из урны вынимают
наугад 5 шаров. Заданы события:
3). Из урны вынимают
наугад 5 шаров. Заданы события:
A={ среди отобранных равно 2 белых и 3 черных шаров};
B={ среди отобранных хотя бы один шар белый};
Найти P(A) и P(B).
Задача № 2. Рассматриваются 2 партии деталей. В первой содержится N стандартных и n дефектных, а во втором все M детали стандартные. Из первой партии наугад извлекают К деталей, а из второй L. Делают смесь из К+L деталей. Из смеси извлекают одну деталь. Найти вероятность того, что деталь окажется стандартной.
Задача № 3. В урне 8 белых и 6 черных шаров. Из неё наугад извлекают 2 шара без возвращения. Рассматриваются случайные величины:
X={ число белых шаров в выборке};
Y={ число черных шаров в выборке};
Необходимо рассмотрим X и Y как систему (x,y), описать и исследовать её.
Решение:
Задача 1)
a) n=C5a+b=(a+b)*(a+b-1)*(a+b-2)*(a+b-3)*(a+b-4) / 5! m=C2aC3b=a*(a-1)*b*(b-1)*(b-2) / 2!*3!
P(A)=m/n=10*a*(a-1)*b*(b-1)*(b-2) / (a+b)*(a+b-1)*(a+b-2)*(a+b-3)*(a+b-4) b) m=C0aC5b=b*(b-1)*(b-2)*(b-3)*(b-4) / 5! P(B)=m/n=b*(b-1)*(b-2)*(b-3)*(b-4) / (a+b)*(a+b-1)*(a+b-2)*(a+b-3)*(a+b-4)
Задача 2)
Гипотезы: H1-изделие в 1 партии, H2-изделие во 2 партии.
P(H1)=K / (K+L), P(H2)=L / (K+L)
P(A)=K*N / (K+L)*(N+n) + L*M / (K+L)*M
Задача 3)
Возможные случаи ={Ч,Ч}{Б,Ч}{Ч,Б}{Б,Б}
|
Y\X |
Ч(0) |
Б(1) |
Σy |
|
Ч(1) |
15/91 |
24/91 |
39/91 |
|
Б(0) |
24/91 |
28/91 |
52/91 |
|
Σx |
39/93 |
52/91 |
1 |
P(Ч,Ч)=6/14 * 5/13=15/91
P(Б,Ч)=8/14 * 6/13=24/91
P(Ч,Б)=6/14 * 8/13=24/91
P(Б,Б)=8/14 * 7/13=28/91
Mx=1*8/14+0*6/14=8/14
My=1*6/14+0*8/14=6/14
Dx=(0-8/14)2 * 6/14 + (1-8/14)2 * 8/14=84/343=48/196
Dx=8/14 – (8/14)2=48/196
Dy=(1-6/14)2 * 6/14 + (0-6/14)2 * 8/14 = 84/343=48/196
Dy=6/14 – (6/14)2=48/196
Kxy=ΣΣ(xi-Mx)(yi-My)=(0-8/14)*(1-6/14)*15/91 + (1-8/14)*(1-6/14)*24/91 + (0-8/14)*(0-6/14)*24/91 + (1-8/14)*(0-6/14)*28/91=84/4459
Гxy=84/4459 * 196/48=1/13
Билет № 4
Задача № 1. В семье двое детей. Порядок записи пар имеет значение и соответствует старшинству. Найти вероятность следующих событий:
А1= {в семье двое мальчиков, при условии, что старший ребенок сын}
А2= { в семье двое мальчиков, при условии, что по крайней мере один сын }
А 3= {в семье хотя бы одна девочка}
Задача № 2. Прибор работает в 2-х режимах: нормальном и ненормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора. Вероятность выхода прибора из строя за время t в нормальном режиме равна 0,1 ,в ненормальном режиме 0,7. Какова вероятность выхода прибора из строя за время t.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.