Математика \ Теория вероятностей и математическая статистика

Решение задач из экзаменационных билетов № 1-25 по курсу "Теория вероятностей и математическая статистика", страница 4

Решение:

Задача №1

а)

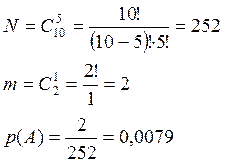
б)

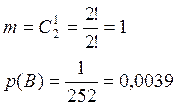
в)

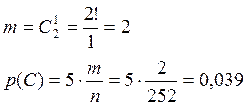
Задача №2

H1-к отличнику

H2- к хорошисту

H3- к посредственно

H4 - к плохо подготовленному

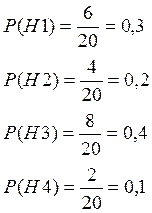
A{студент ответил на 3 вопроса}

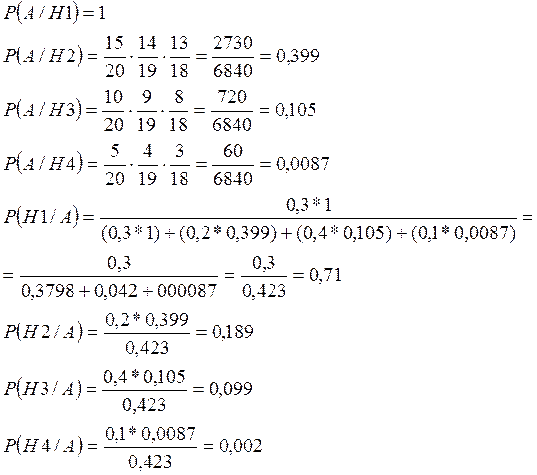
P(H1/A) больше остальных => отличник

Задача №3

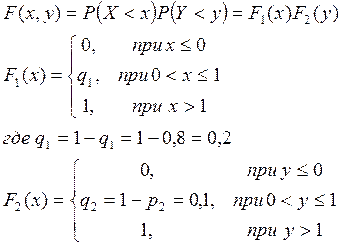
Значения функции F(x,y) даны в таблице

x        y

x=0

0<x<=1

1<x

x<=0

0

0

0

0<y<=1

0

q1*q2=0,02

q2=0,1

1<y

0

q1=0,2

1

Билет № 8

Задача № 1.  Партия деталей содержит N изделий, среди них n бракованных. Для контроля наугад отбирают S деталей. При проведение контроля оказалось, что первые r деталей бракованные. Какова вероятность того, что следующее контролируемое изделие окажется бракованным?

Задача № 2.   Два стрелка стреляют по одной мишени, делая по одному выстрелу. Заданны вероятности попадания для каждого из них и равны соответственно 0,9 и 0,8. После стрельбы в мишень обнаружена одна пробоина. Какой из стрелков пробил мишень?

Задача № 3. .   Один раз подбрасывается игральная кость. Заданы следующие случайные события:

X={  индикатор четного числа очков,};

Y={ индикатор числа очков, кратного 3};

Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её.

Решение:

Задача №1

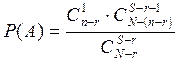
Задача №2

А - попал один из стрелков

H0={промах, промах}

H1={попал, промах}

H2={промах, попал}

H3={попал, попал}

P(H0)=(1-0,8)(1-0,9)=0,02

P(H1)=0,9(1-0,8)=0,18

P(H2)=0,8(1-0,9)=0,08

P(H3)=0,8*0,9=0,72

P(A/H0)=0

P(A/H1)= P(A/H2)=P(A/H3)=1

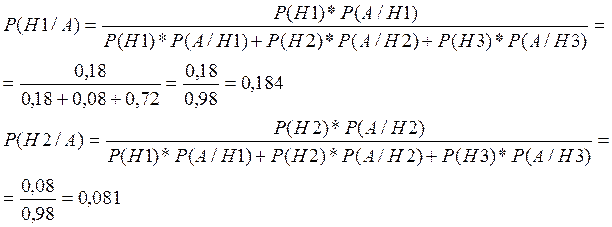
Наиболее вероятно, что попал 1-ый стрелок.

Задача №3

X={  индикатор числа очков, кратного 2};

Y={ индикатор числа очков, кратного 3};

X

Y

0

1

0

2/6

2/6

4/6

1

1/6

1/6

2/6

3/6

3/6

1


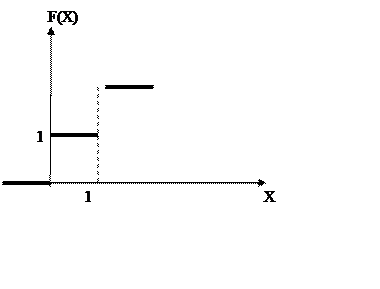
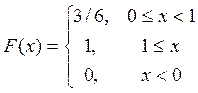
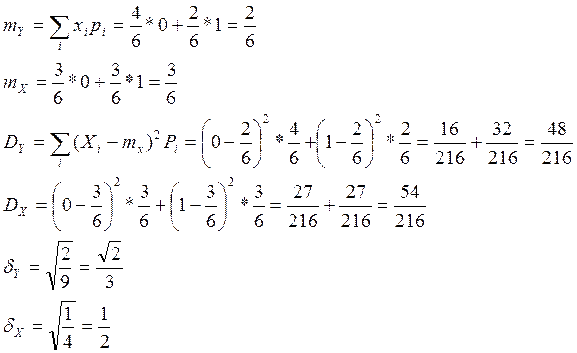
Билет 9

Задача № 1. Из партии деталей , среди которых N стандартных и M бракованных, для контроля наугад отбирают S штук. При контроле оказывалось, что первые k из S деталей стандартные. Определить вероятность того , что следующая деталь будет стандартной.

Задача № 2.   Объект, за которым ведется наблюдение, может в одном из двух состояний:

H1= { он функционирует};

H2= { он не функционирует };

Априорные вероятности этих состояний P(H1)=0,7 и P(H2)=0,3 Наблюдение ведут 2 источника информации и дают такие сообщения : 1-й объект не функционирует; 2-й объект  функционирует. Первый имеет надежность 0,9 ,а второй- 0,7. Скорее всего в каком состоянии находиться объект?

Задача № 3.  Координаты X иY случайной точки распределенное равномерно внутри прямоугольника с абсциcсами x=0, x=1 и ординатами y=0 ,y=1. Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её, построить необходимые графики и найти вероятность обнаружения точки в области R{(x,y)| x0,5 ,y0,5}.

Решение:

Задача 1)

После того как отобрали k деталей из контрольных изделий и оно оказались стандартными, то в контрольной партии осталось  деталей

P(A)–вероятность того, что среди оставшихся контр. деталей выбранная деталь окажется стандартной

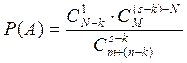
Задание 2

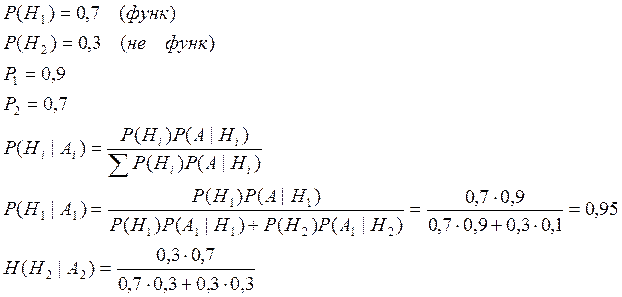
Задание 3

 


 

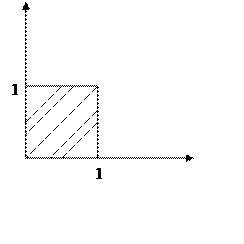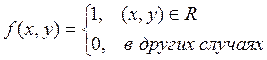
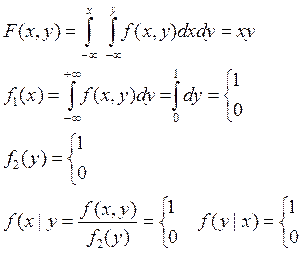
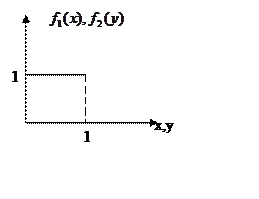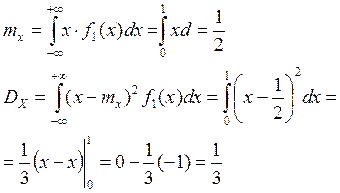
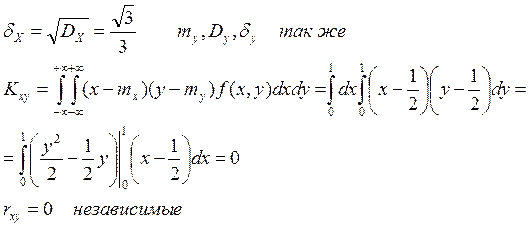
Билет 10

Задача № 1.   Имеется 2 урны, причем в первой 2 белых и 3 черных, во второй 4 и 2 соответственно. Из каждой урны вынимается наугад по одному шару.  Заданны случайные события: 

A={оба шара одного цвета};

B={ шары разных цветов };

Найти P(A), P(B) и проверить вычисления.

Задача № 2.   В партии изделий смешались изделия 3-х заводов: первый выпустил объем N1, N2, N3  - второй и третий соответственно. Заданны вероятности дефекта и они равны соответственно Р1, Р2, Р3. Взяли наугад изделие. Оно оказалось дефектным. Найти вероятность того,  что оно изготовлено 1-м,2-м,3-м заводом.  

Задача № 3.   Субъект №1 и №2 извлекают по одному шару из урны, которая содержит 5 белых и 5 черных шаров. Субъект №1 выбирает наугад шар первым. Заданы следующие случайные события:

X={ число чёрных шаров y №1};

Y={ число чёрных шаров y №2};

Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её. Найти mx|y=1.

Решение:

Задание 1)

A={оба шара одного цвета}

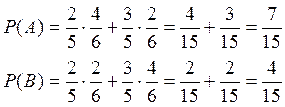
Задание 2)

A={деф. деталь}

Скачать файл