Математика \ Теория вероятностей и математическая статистика

Решение задач из экзаменационных билетов № 1-25 по курсу "Теория вероятностей и математическая статистика", страница 9

б) α2 = 02*7/15 + 12*7/15 + 22*1/15 = 7/15 + 4/15 = 11/15

Dx = 11/15 – 9/25 = (275 - 135)/375 = 140/375 = 28/75

σx = √ Dx = 0.611

Задача 3)

Площадь квадрата равна 4 поэтому

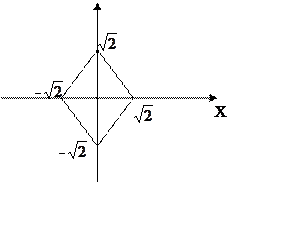
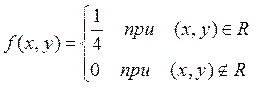
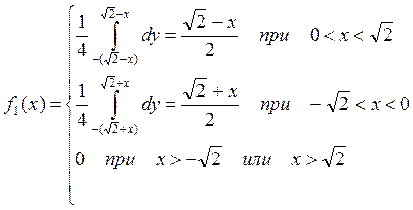
Или иначе

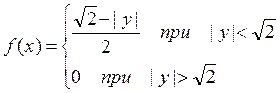
Далее при

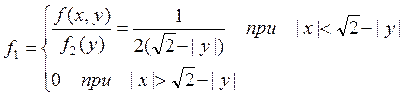
Аналогично при

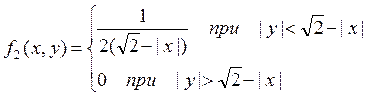
Случайные величины X,Y зависимы, но не коллерированы.

 



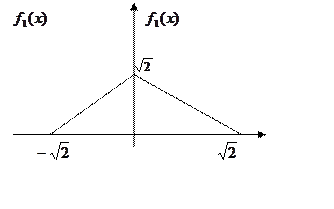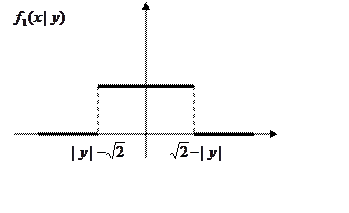Билет № 23

Задача № 1.  Из партии деталей, а в ней n стандартных и m бракованных деталей. Наугад выбирают для контроля S штук. При контроле оказалось, что первые k из S деталей бракованные. Определить вероятность того, что следующая деталь будет бракованной.

Задача № 2.  Поезда нашего метрополитена идут  регулярно с интервалом 4 мин. Студент выходит на платформу в случайный момент времени. Сколько времени он в среднем ожидает поезда? Найти вероятность событий Р{T<2}. Привести поясняющие графики.

Задача № 3.  Бросается две одинаковые  игральные кости. Заданы случайные величины

X={ индикатор четности суммы выпавших очков}

Y={ индикатор появления 2-х шестерок};

Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её.

Решение:

Задание 1

В партии n стандартных и m нестандартных деталей. Выбирают S штук. K из S – брак.  

После того как выбрали k деталей из контрольных изделий и они оказались брак, то в контролир. Партии осталось  деталей.

P(A)- вероятность того что среди оставшихся контр. изделия выбранная деталь окажется браком

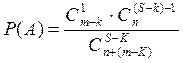
Задание 2.

Приход студента через X.

Приход поезда через Y.

Для того чтобы студент уехал в течение двух минут

 

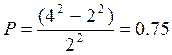
Билет №  24

Задача № 1.  Два стрелка делают по мишени по одному выстрелу. Вероятности попадания для каждого из них при одном выстреле известны и равны 0,9 и 0,95 соответственно. Определить вероятность хотя бы одного попадания в мишень. Проверить полученный результат.

Задача № 2.  Случайная величина X распределена по закону прямоугольного треугольника в интервале (0,а). Описать и исследовать её. Найти вероятность попадания случайной величины X на участке от 0 до а/2. Построить поясняющие графики.

Задача № 3.  Один раз подбрасывается игральная кость. Заданы случайные величины:

X={ индикатор числа очков, кратного 3}

Y={ индикатор четного числа выпавших очков};

Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её.

Решение:

Задание 1.

промах первого стрелка

промах второго стрелка

P()–вероятность промаха первого стрелка

P()–вероятность промаха второго стрелка

                     

События и независимые

 – вероятность одновременного промаха двух стрелков

Событие противоположное  заключается в поражении цели хотя бы одним стрелком.

Искомая вероятность .

Задание 2

 


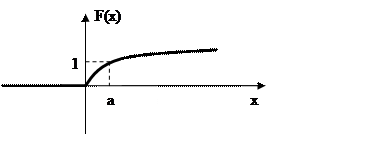
a)  Плотность распределения

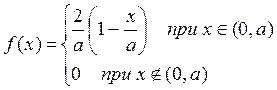
b)  Функция распределения

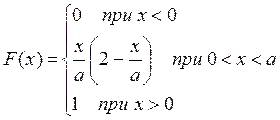
c)  Вероятность попадания случайной величины X на участок 0/0 до

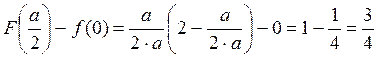
3)Если Х<=0,то F(X)=0:

F(X)=

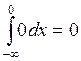
Если

F(X)=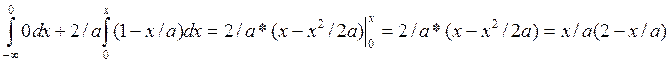

Если X>a,то:

F(x)=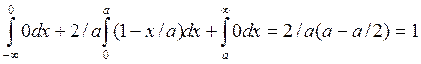

F(x)=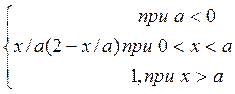

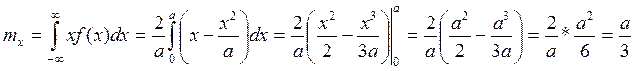
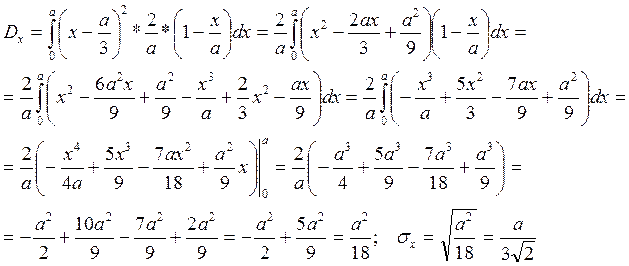
Задание 3)

X={  индикатор числа очков, кратного 2};

Y={ индикатор числа очков, кратного 3};

X

Y

0

1

0

2/6

2/6

4/6

1

1/6

1/6

2/6

3/6

3/6

1


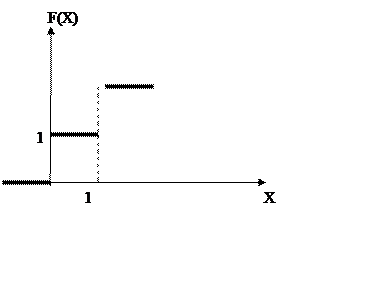
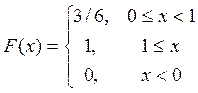
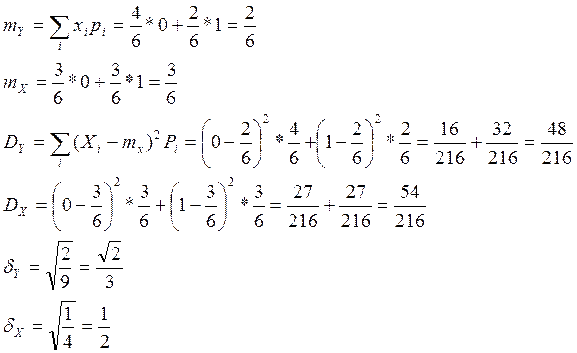
Билет №25

Задача № 1.  Партия включает 100 изделий, среди них 5 бракованных. Отбирают для контроля наугад 50 изделий. Условиями приёма допускается бракованных не более одного из пятидесяти. Определить вероятность того, что партия будет принята.

Задача № 2.  Имеется 2 партии деталей. В первой все детали стандартные, во второй ¼ бракованных. Выбирают наугад партию, извлекают одну деталь и она оказывается бракованной. Какой партии скорее всего принадлежит эта деталь?

Задача № 3.  Два стрелка делают по 2 одиночных выстрела каждый по своей мишени. Вероятность попадания при одном выстреле для них заданы: для первого 0,8 , для второго 0,9.

Заданы случайные величины:

X={ число попаданий первого стрелка}

Y={ число попаданий второго стрелка };

Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её. Найти M[X|Y=1].

Решение:

Задача 1)

95 стандартные, 5 брак, отбирают 50. Всего вариантов выбрать 50 из 100 -  вариантов, чтобы было не более одного брака: ;

Взяли из станд.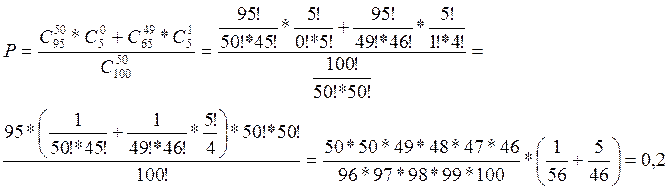

Задание 2

Детали приняты из второй партии

Скачать файл