Решение задач из экзаменационных билетов № 1-25 по курсу "Теория вероятностей и математическая статистика", страница 2

Задача № 3.   Случайная точка А , изображает объект на круглом экране радиолокатора радиуса R=2, равномерно распределена в пределах этого круга. Найти совместную плотность в полярных координатах точки А, описать и исследовать систему. Найти вероятность того, что точка А будет застигнута в положительном квадранте.

Решение:

Задача 1)

Возможные случаи ={М,М}{М,Д}{Д,М}{Д,Д}

P(A1)=1/2,     P(A2)=1/3,     P(A3)=1/4

Задача 2)

P=0.8*0.1+0.2*0.7=0.22

Задача 3)

Билет №5

Задача № 1.    Имеются 2 партии деталей. В первой содержится N , причем среди них  n дефектных, а во втором  M и m соответственно. Из каждой партии  вынимают по  детали. Заданы события

A={ обе детали бракованные};

B={ обе детали стандартные};

Найти P(A) и P(B).

Задача № 2.    Для контроля продукции из трех партий деталей взята наугад для испытания одна деталь. Состав партий таков: в одной – 2/3 брака, а в двух других- все доброкачественные. Какова вероятность, что деталь будет забракована.

Задача № 3.   Один раз подбрасывается игральная кость. Заданы следующие случайные события:

X={  индикатор числа очков, кратного 2};

Y={ индикатор числа очков, кратного 3};

Рассмотрим случайные величины X и Y как систему  (x,y), описать и исследовать её.

Решение:

Задача 1)

Решение найдем для каждой партии отдельно

Для первой партии

А– {бракованное}

В– {стандартное}

Вероятность извлечения стандартного изделия

P(B)=1-P(A)

Найдем Р(А). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно . Число дефектных соответственно ; из этого числа деталей можно  способами извлечь одну нестандартную деталь. Поэтому вероятность того, что извлечена нестандартная деталь равна .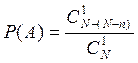

Искомая вероятность .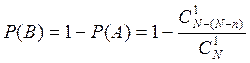

Вероятность извлечения  бракованного изделия.

А– {бракованное}

В– {стандартное}

P(А)=1-P(В)

Найдем Р(В). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно ,соответственно, из этого числа деталей можно  способами извлечь одну стандартную деталь. Поэтому вероятность того, что извлечена стандартная деталь равна .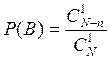

Искомая вероятность .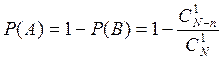

Для второй партии

А– {бракованное}

В– {стандартное}

Вероятность извлечения стандартного изделия

P(B)=1-P(A)

Найдем Р(А). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно . Число дефектных соответственно ; из этого числа деталей можно  способами извлечь одну нестандартную деталь. Поэтому вероятность того, что извлечена нестандартная деталь равна .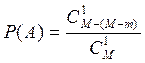

Искомая вероятность .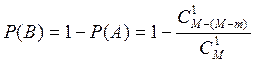

Вероятность извлечения  бракованного изделия.

А– {бракованное}

В– {стандартное}

P(А)=1-P(В)

Найдем Р(В). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно ,соответственно, из этого числа деталей можно  способами извлечь одну стандартную деталь. Поэтому вероятность того, что извлечена стандартная деталь равна .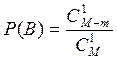

Искомая вероятность .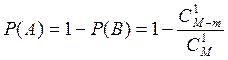

Делаем вывод для обоих партий

Вероятность нахождения обоих стандартных деталей равна: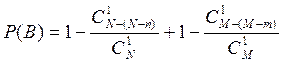

Вероятность нахождения обоих бракованных деталей равна:

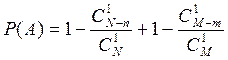
PS: Антона решение

A={обе детали деф.}

B={обе стандартные}

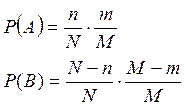
Задача 2)

A={деталь бракована}

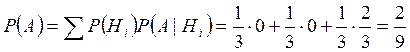
Задача 3)

X={  индикатор числа очков, кратного 2};

Y={ индикатор числа очков, кратного 3};

X Y	0	1
0	2/6	2/6	4/6
1	1/6	1/6	2/6
	3/6	3/6	1

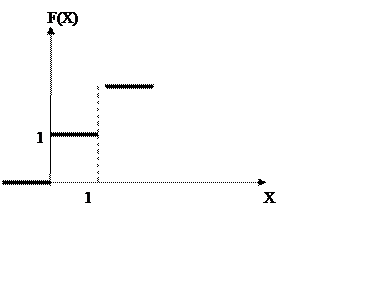
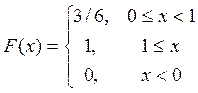
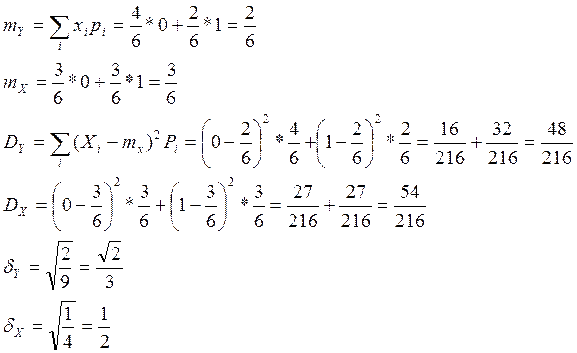
Билет №6

Задача № 1.    Одна партия деталей содержит  а стандартных деталей, причем среди них  b дефектных, а во второй  с и d соответственно . Из каждой партии  вынимают по  детали. Заданы события

A={ обе детали бракованные};

B={ обе детали стандартные};

Найти P(A) и P(B).

Задача № 2.    Имеются две партии изделий по 10 и 12 штук, причем в каждой партии одно изделие бракованное. Из первой партии наугад выбирают одно и перекладывают его во вторую. Из второй наугад извлекается одно изделие. Какова вероятность того, что выбранная деталь окажется бракованной (годным)?