Решение задач из экзаменационных билетов № 1-25 по курсу "Теория вероятностей и математическая статистика", страница 6

P(A)=0,8 вер. попадание в мишень

	0	1	∑y
0	0.04	0.16	0.2
1	0.16	0.64	0.8
∑x	0.2	0.8	1

P₀₀=0,2*0,2=0,04

P₁₀=0,8*0,2=0,16

P₀₁=0,2*0,8=0,16

P₁₁=0,8*0,8=0,64

m_x=0,2*0²+0,8*1²                                                   m_y=0,2*0²+0,8*1²

а) D_x=(0-0,8)²*0,2+0,8*(1-0,8)²=0.16                      D_y=(0-0,8)²*0,2+0,8*(1-0,8)²=0.16

б)  α=0²*0,2+1²*0,8=0,8                                          α=0²*0,2+1²*0,8=0,8

D_x=0,8-0,8²=0,16                                                  D_y=0,8-0,8²=0,16

  σ_x= 0.4                                                                   σ_x = 0.4

K_xy=∑∑(x_i-m_x)(y_i-m_y)=0

r_xy= K_xy/σ_x*σ_y=0

Билет № 13

Задача № 1.  Вычислительное устройство включает n блоков. Вероятность безотказной работы в течение времени T для каждого из них заданы и равны соответственно Р₁,Р₂,…,Р_n. Отход любого блока вызывает отход устройства. Найти вероятность того, что устройство откажет за время T. Какова вероятность, либо отказа не произойдет?

Задача № 2.  Имеется два ящика с шарами. В первом ящике 4 белых и 2 черных, во втором 2 и 4 соответственно. Наугад выбирают ящик и извлекают не глядя из него один шар. Какова вероятность, что выпавший шар окажется белым?

Задача № 3.  Система случайных величин  (x,y)  распределена с постоянной плотностью внутри квадрата R со стороной равной 2,причем стороны составляют углы 45^о с осями координат. Необходимо описать и исследовать систему, построить необходимые графики.

Решение:

Задание 1

– безотказная работа прибора

– устройство не работает

–безотказная работа 1-го блока

– безотказная работа n-го блока

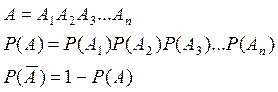
Задание 2

– выбор 1-го ящика

– выбор 2-го ящика

А– появление белого шара

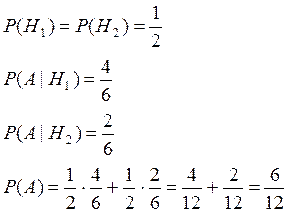
Задание 3

Площадь квадрата равна 4 поэтому

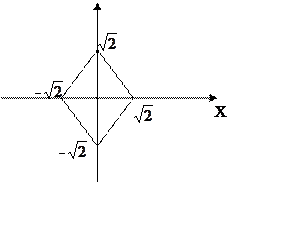
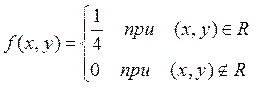
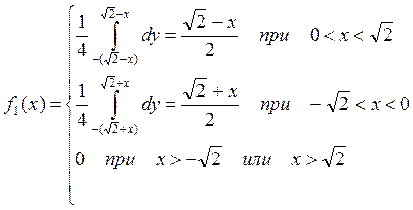
Или иначе

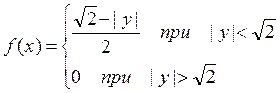
Далее при

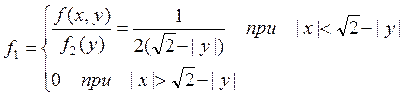
Аналогично при

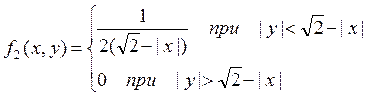
Случайные величины X,Y зависимы, но не коллерированы.

 

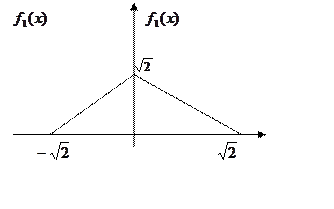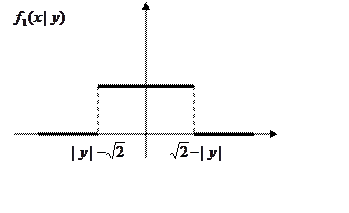Билет №  14

Задача № 1.   Производится три независимых выстрела по мишени. Вероятности попадания заданы и равны Р₁,Р₂, Р₃. Найти вероятность того, что в мишень произойдет ровна два попадания, ( хотя бы одно попадание).

Задача № 2.   Имеются 2 урны: в первой а белых шаров и в черных; во втором с белых и d черных. Из первой урны во вторую перекладывают не глядя один шар. Затем из второй урны наугад вынимают один шар. Какова вероятность того, что этот шар окажется белый?

Задача № 3.  По цели производится два выстрела. Задана вероятность попадания при первом выстреле равна 0,8 , при втором 0,9. 

Заданны случайными величинами: 

X={ число попаданий при первом выстреле };

Y={ число попаданий при втором выстреле};

Рассмотрим  случайные величины X и Y, как систему  (x,y), описать и исследовать её. Оценить к_xy  двумя методами.

Решение:

Задание 1

А– ровно 2 попадания

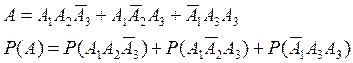
В–хотя бы одно попадание

– ни одного попадания в мишень

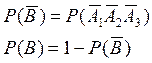
Задание 2

А– вытащили белый

–из 1-го достают белый

–из 1-го достают черный

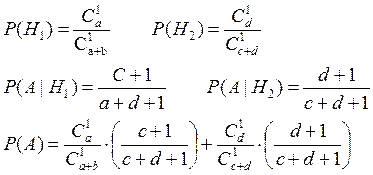
– из 2-ой урны достают белый шар

– извлечен белый шар из 1-ой урны

– извлечен белый шар из 2-ой урны

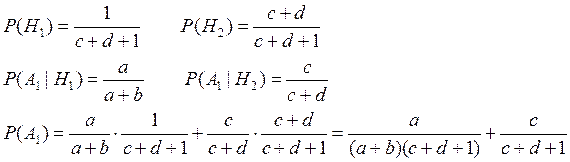
Задание 3

 

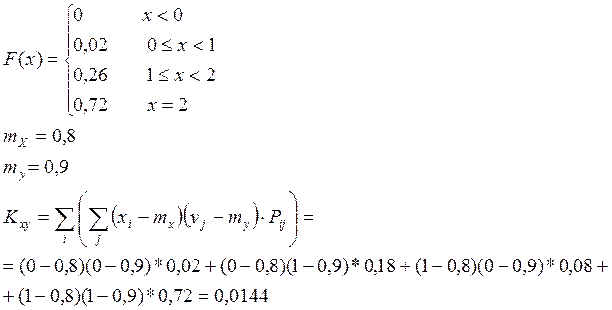
Билет №15

Задача № 1.  Завод изготовляет изделия, при этом каждое из них может иметь дефект с вероятностью  Р₁. Для контроля отбирают n изделий  наугад. При контроле дефект, если он существует, обнаруживается с вероятностью Р₂. Найти вероятность того, что ни в одном из изделий не обнаружено дефекта.

Задача № 2.   Приборы одного наименования изготовляются двумя заводами: первый завод поставляет 2/3 всех изделий на производство; второй – 1/3. Надежность прибора от 1-го завода 0,9 , от второго 0,85. Определить полную надежность прибора, поступившего на производство.

Задача № 3.  . Из урны, которая  содержит 10 белых и 5 черных шаров, наугад извлекают 2 шара без возращения. Заданны случайные величины: 

X={ число белых шаров в выборе};

Y={ число черных шаров в выборе};

Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её. Найти ряд распределения для условной вероятности случайной  величины Y при условии, что x=0.

Решение

Задача № 1.

А = {ни в одном из n отобранных изделий дефекта е обнаружено} Р(А) - ?