Решение задач из экзаменационных билетов № 1-25 по курсу "Теория вероятностей и математическая статистика", страница 3

Задача № 3.   Число X выбираем случайным образом из множества целых чисел{1,2,3}. Из того же множества выбирают наугад числоY, больше первого или равный ему. Необходимо рассмотреть X и Y как систему, описать и исследовать.

Решение:

Задача 1)

Решение найдем для каждой партии отдельно

Для первой партии

А– {бракованное}

В– {стандартное}

Вероятность извлечения стандартного изделия

P(B)=1-P(A)

Найдем Р(А). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно . Число дефектных соответственно ; из этого числа деталей можно  способами извлечь одну нестандартную деталь. Поэтому вероятность того, что извлечена нестандартная деталь равна .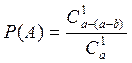

Искомая вероятность .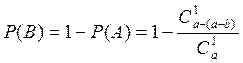

Вероятность извлечения  бракованного изделия.

А– {бракованное}

В– {стандартное}

P(А)=1-P(В)

Найдем Р(В). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно ,соответственно, из этого числа деталей можно  способами извлечь одну стандартную деталь. Поэтому вероятность того, что извлечена стандартная деталь равна .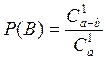

Искомая вероятность .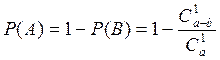

Для второй партии

А– {бракованное}

В– {стандартное}

Вероятность извлечения стандартного изделия

P(B)=1-P(A)

Найдем Р(А). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно . Число дефектных соответственно ; из этого числа деталей можно  способами извлечь одну нестандартную деталь. Поэтому вероятность того, что извлечена нестандартная деталь равна .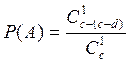

Искомая вероятность .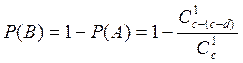

Вероятность извлечения  бракованного изделия.

А– {бракованное}

В– {стандартное}

P(А)=1-P(В)

Найдем Р(В). Общее число способов которыми можно извлечь 1 деталь из N деталей равно . Число стандартных деталей равно ,соответственно, из этого числа деталей можно  способами извлечь одну стандартную деталь. Поэтому вероятность того, что извлечена стандартная деталь равна .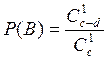

Искомая вероятность .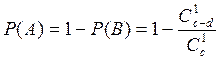

Делаем вывод для обоих партий

Вероятность нахождения обоих стандартных деталей равна: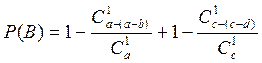

Вероятность нахождения обоих бракованных деталей равна:

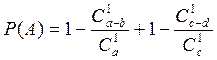
Задача 2)

Случай для годного изделия

Обозначим через А событие {из первой партии извлечено стандартное изделие}.

Из первой партии первой партии могло быть извлечено либо стандартное изделие (событие ), либо нестандартное изделие (событие ).

Вероятность того, что из первой партии извлечено стандартное изделие,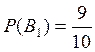

Вероятность того, что из второй партии извлечено нестандартное изделие,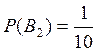

Условная вероятность того, что второй партии извлечена стандартная деталь, при условии, что из первой партии перенесена во вторую стандартная деталь, равна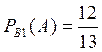

Условная вероятность того, что второй партии извлечена стандартная деталь, при условии, что из первой партии перенесена во вторую нестандартная деталь, равна .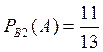

Искомая вероятность того, что из второй партии будет извлечена стандартная деталь, по формуле полной вероятности равна

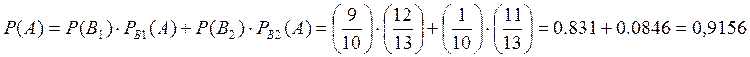
– вероятность извлечения стандартной детали из второй партии.

– вероятность извлечения нестандартной детали из второй партии.

Т.к.  соответственно вероятность того, что из второй партии будет извлечена нестандартная деталь равна

Задача 3)

Билет №  7

Задача № 1. Из 10 билетов выигрышными являются только два. Субъект наугад выбирает 5 билетов. Заданны случайные события: 

A={среди 5 билетов один выигрышный};

B={ среди 5 билетов оба выигрышных };

С={ среди 5 билетов хотя бы один выигрышный  };

Найти P(A), P(B), Р(С).

Задача № 2.   В группе 20 студентов, пришедших на экзамен. Из них 6 подготовлены на отлично, 4 хорошиста, 8 посредственно и 2- плохо подготовлены.  В экзаменационных билетах имеются 20 вопросов. Возможности студентов следующие:

Отличник может ответить на все 20 вопросов, хорошист- на 15, посредствнник- на 10,  плохо подготовленный- на 5. Вызванный наугад студент ответил на 3 поставленных ему вопроса. К какой категории относится  этот студент?

Задача № 3.    По цели производится 2 выстрела. Вероятность попадания при первом выстреле равны Р₁, при втором – Р₂. Случайная величина X- число попаданий при первом выстреле, Y-  число попаданий при втором выстреле.

Рассмотреть  X и Y как систему  (x,y), описать и исследовать её, приняв Р₁=0,8 Р₂ =0,9.