Решение задач из экзаменационных билетов № 1-25 по курсу "Теория вероятностей и математическая статистика", страница 5

B1 - деталь взяли из 1

В2 – делали взяли из 2

В3 – деталь взяли из 3

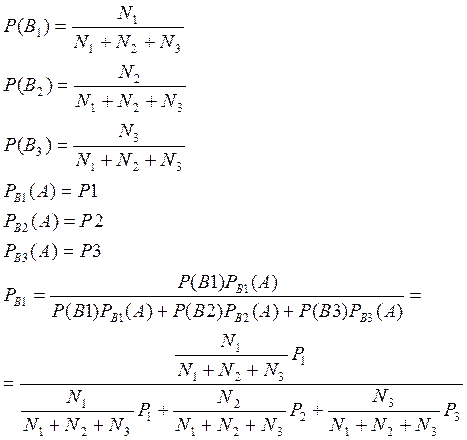
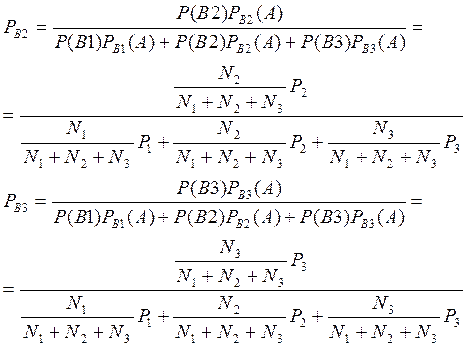
Задание 3)

Билет № 11

Задача № 1.   Над деталью работают последовательно k рабочих. Промежуточного контроля качествам нет. Первый рабочий допускает брак с вероятностью P₁ , второй - с вероятностью P₂ и т.д. После k-ой операции проводят контроль. Найти вероятность того, что при изготовление будет допущен брак, если обнаружение брака достоверное событие,(изделие будет годным).

Задача № 2.  В группе  студентов включает а отличников, в хорошо успевающих и с занимающих слабо.  Отличники могут получить на предстоящем экзамене 5.  Студенты с хорошей успеваемостью могут получить «4» или «5».  Слабо занимающиеся могут получить «2»,«3»,«4». Вызывают наугад студента  Заданно событие:

A={студент получит «4» или «5»};

Найти P(A).

Задача № 3. Из урны, содержащей 4 белых и 6 черных шаров, наугад извлекают 2 шара. Заданны случайными величинами: 

X={ число чёрных шаров в выборе};

Y={ число белых шаров в выборе};

Рассмотрим  X и Y, как систему  (x,y), описать и исследовать её.

Решение:

Задача 1)

Q₁=(1-P₁)- вероятность не появления брака при работе 1 рабочего.

……

……

Q_k=(1-P_k)- вероятность не появления брака при работе k рабочего.

P(x)=q₁*q₂*…*q_k – вероятность, что брака не будет.

P(x₁)=1- q₁*q₂*…*q_k – вероятность, что брака  будет.

Задача 2)

H₁- вызван отличник

H₂- вызван хорошо успевающий.

H₃- вызван занимающийся слабо.

P(H₁)=a/a+b+c

P(H₂)=b/a+b+c

P(H₃)=c/a+b+c

Искомая вер. равна:

P(A)= 1*P(H₁)+ 1*P(H₂)+1/3*P(H₃)= (a+b+1/3*c/a+b+c) 

Задача 3)

Y                       x	0	1	2	∑
0	0	0	2/15	2/15
1	0	8/15	0	8/15
2	5/15	0	0	5/15
∑	5/15	8/15	2/15	1

P_чч=0,6*5/9=1/3

P_бч=0,4*6/9=4/15

P_чб=0,6*4/9=4/15

P_бб=0,4*3/9=2/15

m_y=(2/15)*0+(8/15)*1+2*(5/15)=18/15              m_x=(5/15)*0+(8/15)*1+(5/15)*2=12/15

Расчет дисперсии.

а) D_x=(0-12/15)²*(5/15)+(8/15)*(1-12/15)²+(2/15)*(2-12/15)=0.427                  

D_y=(0-18/15)²*(2/15)+(8/15)*(1-18/15)²+(5/15)*(2-18/15)=0.426  

  σ_x= 0.653                                                                 σ_y = 0.653

Расчет коэф. корреляции

K_xy=∑∑(x_i-m_x)(y_i-m_y)=5/15*(0-12/15)(2-18/15)+8/15*(1-12/15)(1-18/15)+2/15(2-12/15)(0-18/15)=посчитать

R_xy=K_xy/ σ_x σ_y=посчитать. Простая арифметика.

Билет №12

Задача № 1.

Радиолокационная станция следит за космическим объектом. При одном обзоре она обнаруживает объект с вероятностью Р. Станция сделала n циклов обзора.  Какова вероятность , что объект будет при этом обнаружен?, (не будет обнаружен?)

Задача № 2.  По объекту производиться три выстрела. Задана вероятности попадания для этого случая и они соответственно равны Р₁, Р₂, Р_3.  Для вывода объекта из строя достаточно трех попаданий, при двух попаданиях он выходит из строя с вероятностью Р₂ , при одном - Р₁. Найдите вероятность того, что в результате 3-х выстрелов объект будет выведен из строя.

Задача № 3.   Производится два выстрела по мишени, причем вероятность попадания при одном выстреле равна 0,8.

Решение:

Задача 1)

P-вероятность появление объекта.

q=1-P- вероятность не появления объекта.

P(x)=1-qⁿ –объект не будет потерян.

P(x₁)=qⁿ –объект  будет потерян

X-объект будет найден

X₁- объект  не будет найден

Задача 2)

H₀- в объект не попали не разу.

H₁- в объект попали один раз.

H₂- в объект попали два раза.

H₃- в объект попали три  раза.

Пользуясь теоремой сложения и умножения найдем вер. этих гипотез.

P(H₀)=(1-P₁)(1-P₂)(1-P₃)

P(H₁)=P₁*(1-P₂)(1-P₃)+ (1-P₁)*P₂*(1-P₃)+ (1-P₁)(1-P₂)*P₃

P(H₂)= (1-P₁)*P2*P3+ (1-P₂)*P₁*P₃+ (1-P₃)*P₁*P₂

P(H₃)= P₃*P₁*P₂

Условные вероят.  событий  А(выход сам из строя) при этих гипотезах равна.

P(A|H₀)=0

P(A|H₁)=P₁

P(A|H₂)=P₂

P(A|H₃)=1

Применяя формулу полной вероятности получаем:

Ответ: P(A)=P(H₀)*P(A|H₀)+ P(H₁)*P(A|H₁)+ P(H₂)*P(A|H₂)+P(H₃)*P(A|H₃)

Задача 3)

Заданны случайными величинами: 

X={ число выстрелов до 1-го попадания};

Y={ число попаданий};

Рассмотрим  случайные величины X и Y, как систему  (x,y), описать и исследовать её.

Решение: