Решение задач из экзаменационных билетов № 1-25 по курсу "Теория вероятностей и математическая статистика", страница 8

Задача № 1.   При включении двигателя, он может начать работать с вероятностью Р. Задано событие : A={двигатель начинает работать при втором включении} Найти Р(А).

Задача № 2.  Имеется 7 приборов, среди них 3 бракованных. Наугад выбирают 4, проверяют их на качество. Задана случайная величина X={число работающих приборов}. Описать случайную величину и исследовать её.

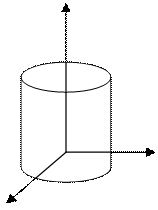
Задача № 3.  Поверхность распределения f(x,y) системы непрерывных случайных величин (x,y) представляет собой прямой круговой цилиндр, центр основания его совпадает с началом координат, а его высота равна 2. Необходимо описать (x,y) и исследовать её.

Решение:

Задача №1

A={двигатель начнет работать со 2-ого включения}

P(A)=(1-p)*p

Задача №2

X={число раб. приборов}

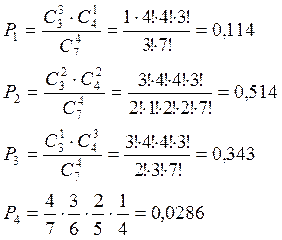
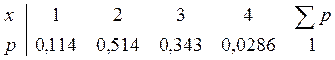
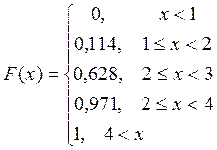
Задача №3

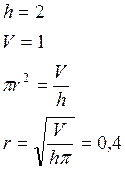
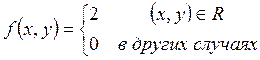
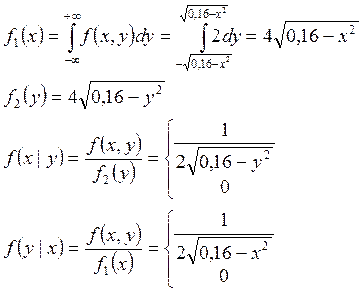
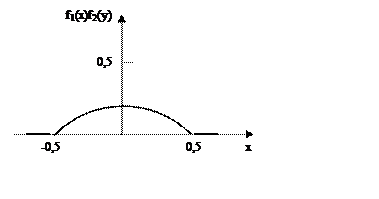
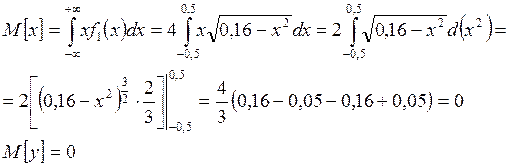
Билет № 19

Задача № 1. При включении зажигания на автомобиле его двигатель начнет работать с вероятностью Р.  Задано событие:

A={для ввода двигателя в работу потребуется не более 2-х раз включения зажигания } Найти Р(А).

Задача № 2.  Дважды подбрасывается монета. Задана случайная величина  X={число выпавших гербов}. Описать случайную величину X и исследовать её.

Решение:

Задача 1)

Обозначим А={включение двигателя в i-ой попытке }

Тогда событие А запишется как

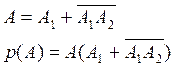
Т.к. события несовместны, то

По теореме о полной группе событий

Тогда искомая вероятность

Задача 2)

Возможные значения X={0; 1; 2}. Имеем дискретную случайную величину.

Составим ряд распределения

1) 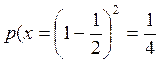, где р=1/2-вероятность выпадения герба в одном подбрасывании.

2)

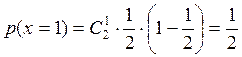
3)

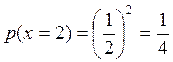
Ряд распределения

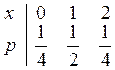
Многоугольник распределения

Функция распределения

Аналитическое выражение для функции распределения

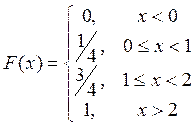
Математическое ожидание

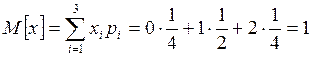
Дисперсия

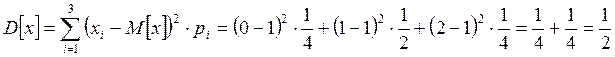
Среднеквадратическое отклонение

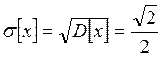
Мода

Задача 3)

Билет № 20

Задача № 1.  В урне  а белых шаров и в чёрных.  Из  урны вынимают один шар,  его цвет отмечается и шар возвращается в урну. Из урны снова берётся ещё один шар. Какова вероятность, что они оба вынутых шара будут белыми?

Задача № 2. Из урны, которая  содержит 3 белых и 2 черных шара, наугад извлекают 3 шара. Заданны случайные величины: 

X={ число чёрных шаров в выборе};

Описать и исследовать случайную величину X.

Решение:

Задача 1)

Рассмотрим первое извлечение

Пусть событие А – появление белого шара

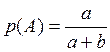- по теореме о непосредственном подсчете вероятностей как отношения числа благоприятных событий к общему числу событий.

Событие В – извлечение белого шара во 2м опыте. Поскольку после первого опыта шар был возвращен обратно в урну. то вероятность осталась прежней.

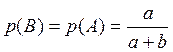
Таким образом имеем 2 независимых события.

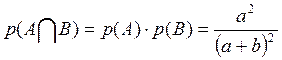
Задача 2)

Возможные значении CD Х={0; 1; 2}

CD распределена по гипергеометрическому закону

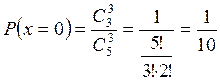 - извлечены 3 белых шара

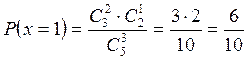 - извлечены 2 белых шара и 1 черный

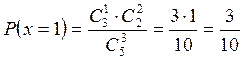 - извлечены 1 белый и 2 черных шара

Ряд распределения

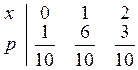
Многоугольник распределения

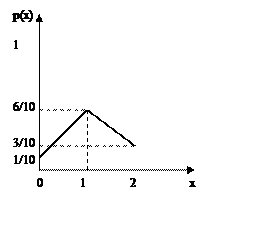
Функция распределения

Аналитическое выражение для функции распределения

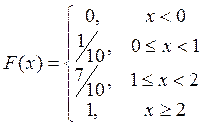
Математическое ожидание

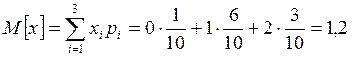
Дисперсия

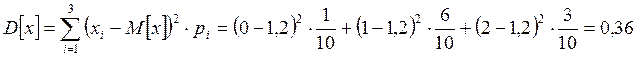
Среднеквадратическое отклонение

Задача 3)

Билет №21

Задача № 1.  Прибор состоит из четырех узлов №1,№2,№3 и №4. Вероятность безотказной работы i-го узла равна Р_i. Заданы события:

А={все узлы работают безотказно};

В={откажет хотя бы один узел};

Найти P(A) и P(B).

Задача № 2. Имеется 10 приборов, среди них 2 дефектных. Наугад выбирают 3, проверяя их качество. Задана случайная величина X={число бракованных приборов} Описать случайную величину X и исследовать её.

Задача № 3.  Случайная точка (X;Y) распределена с постоянной плотностью внутри квадрата R, со сторонами, составляющими 45^о с осями координат, а длина стороны равна 2.  Необходимо описать и исследовать систему (X,Y).

Решение:

Задача 1:

Прибор из четырех узлов

p_i – вероятность безотказной работы i-го узла

A = {все узлы работают безотказно}

B = {откажет хотя бы один узел}

P(A) = p₁p₂p₃p₄

P(B) = 1 - p₁p₂p₃p₄

Задача 2:

10 приборов, 2 дефектных, вынимают три наугад

X = {число бракованных приборов}

xi	0	1	2
pi	7/15	7/15	1/15

p₀ = (C⁰₂*C³₈)/C³₁₀ = 56/120 = 7/15

p₁ = (C¹₂*C²₈)/C³₁₀ = 56/120 = 7/15

p₂ = (C²₂*C¹₈)/C³₁₀ = 8/120 = 1/15

 

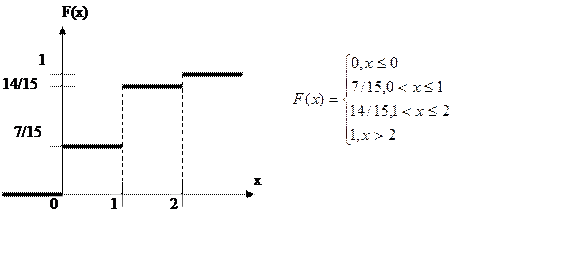
m_x = 0*7/15 + 1*7/15 + 2*1/15 = 9/15 = 3/5

а) D_x = (0-3/5)²*7/15 + (1-3/5)²*7/15 + (2-3/5)²*1/15