Р(А) = Р(дефекта нет, и он не обнаружен) + Р(дефект есть, но он не обнаружен)
дефекта нет, и он не обнаружен: обратное событие: дефект есть, и он обнаружен: (Р1*Р2)n
дефекта нет, и он не обнаружен: (1-Р1*Р2)n
дефект есть, но не обнаружен: Р![]() * (1-Р2)n
* (1-Р2)n
Р(А) = (1-Р1*Р2)n + Р![]() * (1-Р2)n
* (1-Р2)n
Задача № 2.
Р = ![]() *0,9 +
*0,9 + ![]() *0,85 = 0,6 + 0,283 = 0,883
*0,85 = 0,6 + 0,283 = 0,883
![]()
Задача № 3.
x={число
белых}; y={число белых}; ![]() ;
; ![]()
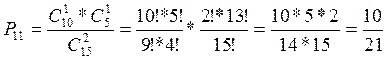
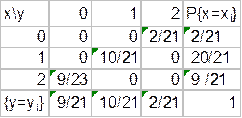 ;
;
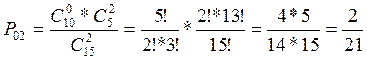 ;
;
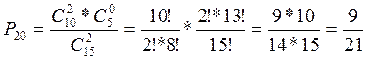
![]()
![]() 0, x≤0 0,
x≤0
0, x≤0 0,
x≤0
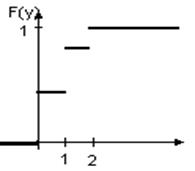
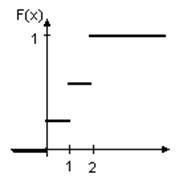
F(x)= 2/21, 0<x≤1 ; F(y)= 9/21, 0<x≤1 ;
12/21, 1<x≤2 19/21, 1<x≤2
1, x>2 1, x>2
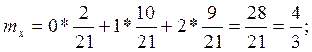
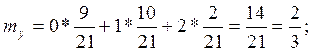
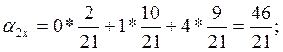
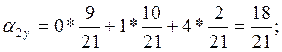
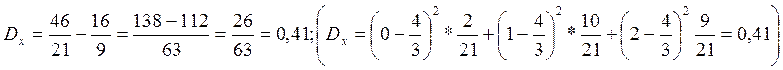 ;
; ![]()
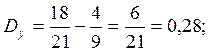
![]()
![]() ,
, 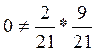 следовательно зависимы;
следовательно зависимы;
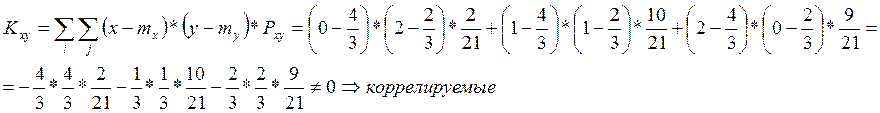
Билет №16
Задача № 1. Производится n независимых опытов, в каждом из которых событие А может появится с вероятностью Р. Найти вероятность того, что вероятность событие А появится хотя бы один раз.
Задача № 2. Имеются две урны : в первой а белых
шаров и в чёрных; во второй с и d соответственно. Из
первой урны во вторую перекладывают 3 шара. (а![]() 3, в
3, в![]() 3) Наугад из второй извлекают один шар.
Какова вероятность, что он будет белым?
3) Наугад из второй извлекают один шар.
Какова вероятность, что он будет белым?
Задача № 3. Координаты X иY случайной точки распределенное равномерно внутри
прямоугольника с абциcсами x=1,
x=3 и ординатами y=1 ,y=4. Рассмотрим X и Y, как систему (x,y),
описать и исследовать её. Найти вероятность появления случайной точки (x,y) в области R,
где R={(x,y)|
(x![]() 2, y
2, y![]() 3)}. Построить необходимые графики.
3)}. Построить необходимые графики.
Решение
Задача № 1.
А1 = {событие А появится хотя бы один раз}
![]() = {ни одного раза не появится}
= {ни одного раза не появится}
Р1(![]() ) = (1-Р)n
) = (1-Р)n
Р1(А1) = 1 - (1-Р)n
Задача № 2.
А = {вытянутый из 2-ой урны шар белый}
Н1 = {вытянутый из 2-й урны шар принадлежит 1-ой урне}
Н2 = {вытянутый из 2-й урны шар принадлежит 2-ой урне}
Так как во второй урне три шара принадлежат первой урне, то:
Р(Н1) = 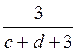
Р(Н2) = 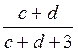
Вероятность появления белого шара из 2-ой урны не зависит от того, вынимается ли этот шар непосредственно из 1-ой урны или после перекладывания во вторую, поэтому:
Р(А![]() ) =
) = ![]()
Р(А![]() ) =
) = 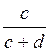
Р(А) = 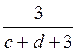 *
*![]() +
+
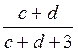 *
*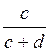
Задача № 3.
![]() f(x,y)=
f(x,y)=![]() C, (x,y)
C, (x,y)![]() D
D
0, в ост. случаях
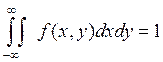
Площадь прямоугольника равна 6, поэтому С = ![]()
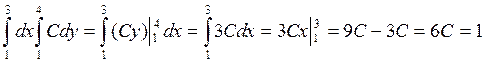 ; С =
; С = ![]()
![]() f(x,y)=
f(x,y)=![]()
![]() , (x,y)
, (x,y)![]() D
D
0, в ост. случаях
F(x,y) = 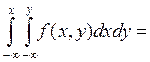
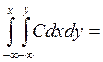
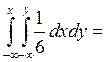
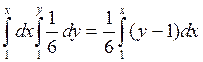 =
=
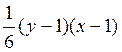
![]() F(x,y)=
F(x,y)=![]()
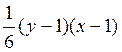 ,
(x,y)
,
(x,y)![]() D
D
0, в ост. случаях
![]() f1(x)=
f1(x)=![]()
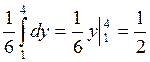 , x
, x![]() (1,3)
(1,3)
0, x<1![]() x>3
x>3
![]() f2(y)=
f2(y)=![]()
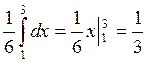 , y
, y![]() (1,4)
(1,4)
0, y<1![]() y>4
y>4
F1(x)
= 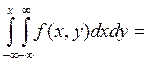
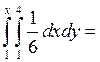
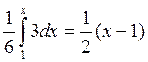
![]() F1(x)=
F1(x)=![]()
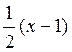 , (x,y)
, (x,y)![]() D
D
0, в ост. случаях
F2(y)
= 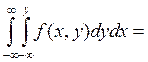
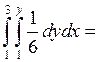
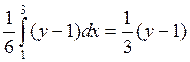
![]() F2(y)=
F2(y)=![]()
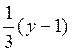 , (x,y)
, (x,y)![]() D
D
0, в ост. случаях
![]() f1(x
f1(x![]() ) =
) = 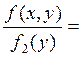
![]()
![]() ,
(x,y)
,
(x,y)![]() D
D
0, в ост. случаях
![]() f2(y
f2(y![]() ) =
) = 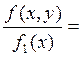
![]()
![]() ,
(x,y)
,
(x,y)![]() D
D
0, в ост. случаях
m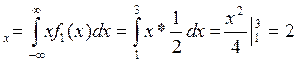
m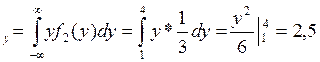
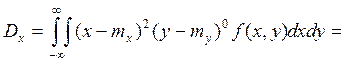
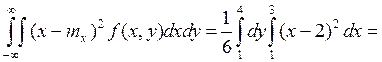
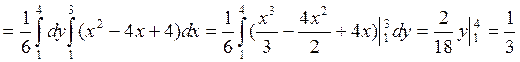
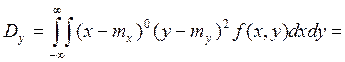
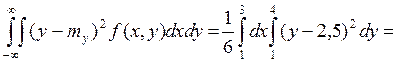
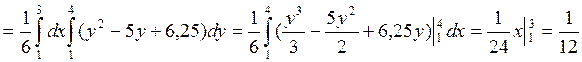
Зависимость/независимость:
f(x,y) = f1(x)*f2(y); 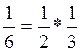 , следовательно, величины независимы
, следовательно, величины независимы
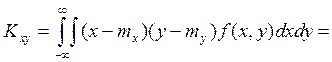
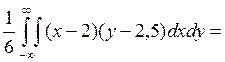
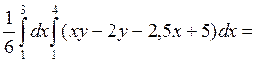
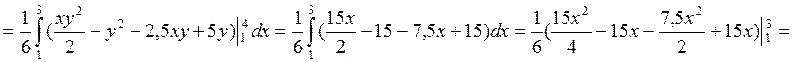
=![]() (30-30-30+30) = 0, следовательно,
величины некоррелированные
(30-30-30+30) = 0, следовательно,
величины некоррелированные
Р((x,y)![]() R) =
R) = 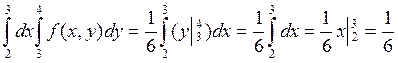
Билет № 17
Задача № 1. Вычислительная машина состоит из n блоков. Вероятность безотказной работы в течение времени T первого блока равна Р1, второго Р2 и т.д. При отказе любого блока отказывает и машина. Найти вероятность того, что машина откажет за время T.
Задача № 2. Спортсмен производит два выстрела по мишени. Вероятность попадания при одном выстреле равна Р. Заданы случайная величина X={ разность между числом попаданий и числом промахов}. Описать случайную величину X и исследовать её при Р=0,8.
Задача № 3. Передаются 2 сообщения, каждое из них может искажено или не искажено. Заданы события: A={сообщение искажено} , причем для первого сообщения Р(А)=0,8 , а для второго – 0,9. Система (x,y) задана таким образом:
X={ 1, если первое сообщение искажено
0, если первое сообщение не искажено ;
Y={ 1, если второе сообщение искажено
0, если второе сообщение искажено };
Рассмотрим X и Y, как систему (x,y), описать и исследовать её.
Решение:
Задача №1
A={Система откажет}
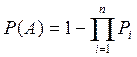
Задача №2
X={разность числа попаданий и промахов}
pпоп.=0,8
2 промаха: P-2=0,2*0,2=0,04
1 промах: P0=2*0,2*0,8=0,32
0 промахов: P2=0,8*0,8=0,64
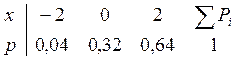

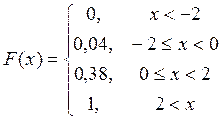
![]()
a) ![]()
b) ![]()
![]()
![]()
Задача №3
A={событие искажено}
P1(A)=0,8
P2(A)=0,9
X={искажено 1-ое}
Y={искажено 2-ое}
P0,0=0,2*0,1=0,02
P1,0=0,8*0,1=0,08
P0,1=0,2*0,9=0,18
P1,1=0,8*0,9=0,72
|
Y X |
0 |
1 |
∑Y |
|
0 |
0,02 |
0,08 |
0,1 |
|
1 |
0,18 |
0,72 |
0,9 |
|
∑X |
0,2 |
0,8 |
1 |
![]()
a) ![]()
b) ![]()
![]()
![]()
![]()
a) ![]()
b) ![]()
![]()
![]()
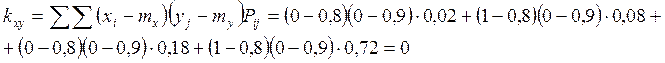
Не коррелированные
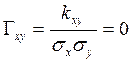
Билет № 18
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.