Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации

1 Методы одномерной оптимизации

Задача оптимизации, в которой критерий оптимальности задан функцией одной переменной, часто встречается в инженерной практике. Кроме того, одномерные методы оптимизации часто используются при решении подзадач многомерной оптимизации. Поэтому анализ задач такого типа занимает центральное место в оптимизационных исследованиях. Это обусловило разработку большого числа методов одномерной оптимизации. Ниже рассматриваются некоторые из этих методов. При этом приводятся алгоритмы поиска максимума целевой функции I(x), где x – параметр оптимизации. Учитывая, что минимуму функции I(x) соответствует максимум функции -I(x), т. е.  то изменив знак y минимизируемой функции I(x) на обратный, алгоритмами поиска максимума можно пользоваться и для поиска минимума I(x).

1.1  Одномерная оптимизация методом классического анализа

Методы классического анализа применяются для решения задач оптимизации в том случае, когда целевая функция и ограничения заданы аналитически в виде непрерывных дифференцируемых функций.

Математическая формулировка задачи оптимизации часто эквивалентна задаче отыскания экстремума функции одной или многих переменных. Поэтому для решения таких оптимальных задач могут быть использованы различные методы исследования функций классического анализа и, главным образом, методы поиска экстремума.

Пусть зависимость критерия оптимальности от переменной x задана непрерывной функцией

                                        (1.1)

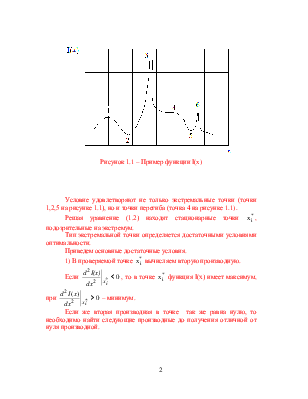
Функция I(x) может иметь экстремальные значения при таких значениях независимой переменной x, где производная функции I(x) равна нулю (точки 1,2,5 на рисунке 1.1), либо вообще не существует (точки 3,6 на рисунке 1.1):

                                                (1.2)

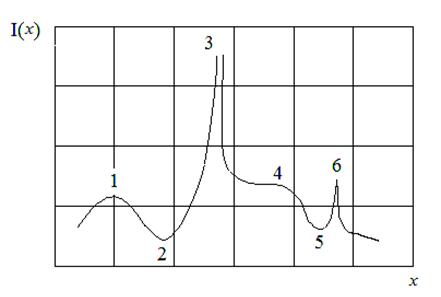
Рисунок 1.1 – Пример функции I(x)

Условие удовлетворяют не только экстремальные точки (точки 1,2,5 на рисунке 1.1), но и точки перегиба (точка 4 на рисунке 1.1).

Решая уравнение (1.2) находят стационарные точки , подозрительные на экстремум.

Тип экстремальной точки определяется достаточными условиями оптимальности.

Приведем основные достаточные условия.

1) В проверяемой точке  вычисляем вторую производную.

Если 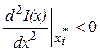, то в точке  функция I(x) имеет максимум, при 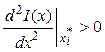 – минимум.

Если же вторая производная в точке  так же равна нулю, то необходимо найти следующие производные до получения отличной от нуля производной.

Пусть 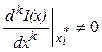, , 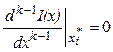k=2,3,4…

Если k – нечетное, то в точке  экстремума нет, если k – четное, тогда:

при 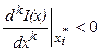, в точке функция I(x) имеет максимум;

при 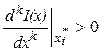 – минимум.

2) Определяем знак производной слева и справа от точки. При переходе этого знака с «+» на «-» – в точке  – максимум, при переходе «-» на «+» – в точке  – минимум.

3) Тип экстремальной точки можно определить путем сравнения величины функции I(x) слева и справа от точки :

если , то  является точкой максимума, а

если , то  – точка минимума.

При решении практических задач оптимизации обычно требуется отыскать глобальный экстремум критерия I(x). В этом случае необходимо:

1) найти все точки функции I(x) в которых может быть экстремум;

2) исследовать все эти точки на экстремум;

3) среди локальных экстремумов нужного типа найти глобальный.

При наличии большого числа точек , для уменьшения объема вычислений при проверке экстремальности этих точек достаточно «подозрительные» точки проверять через одну, что позволяет установить тип всех экстремумов функции I(x), так как для непрерывных функций одной переменной максимумы и минимумы чередуются между собой.

1.2  Метод равномерного поиска

Пусть априорная информация об унимодальности функции крайне недостаточна, чтобы строить разумный процесс поиска экстремума. Наиболее приемлемым способом поведения в такой обстановке является последовательное вычисление целевой функции I(x) при всех допустимых значениях варьируемого параметра x

a £ x £ b ,

где a, b – границы интервала поиска.

Пусть d заданная величина погрешности определения оптимального параметра x*. Тогда для реализации алгоритма поиска следует определить значение I(x) в  точках, равномерно отстоящих друг от друга на расстоянии h = d, т. е. в точках   

Из полученных значений показателя качества I(x_j) выбирается наибольшее значение (глобальный максимум). Такой способ поиска называется сканированием. При малой заданной погрешности d этот метод требует слишком большое число вычислений функции I(x) и больших затрат машинного времени.

1.3  Метод поразрядного приближения

Этот метод применим для поиска оптимума унимодальной функции и обладает более высоким быстродействием. Это достигается тем, что используется алгоритм с переменным шагом поиска. Вначале величина шага выбирается достаточно большой, значительно превышающей требуемую погрешность определения положения оптимума, и выполняется грубый поиск. В районе оптимума поиск производится с меньшим шагом.

Рассмотрим алгоритм такой стратегии поиска максимума функции I(x). Пусть интервал [a,b] содержит внутри себя максимальное значение параметра x*: a £ x* £ b.

Задается начальное значение параметра x₀ = a и вычисляется I₀=I(x₀). Задаются начальный шаг поиска h и кратность k уменьшения шага в районе оптимума. Производится поиск максимума I(x) из начальной точки x=x₀ по алгоритму:

x(j+1)=x(j)+h(j+1);

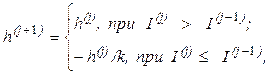                      (1.3)

где  j – номер шага.

Поэтому алгоритму поиск из начальной точки x = x₀ осуществляется с постоянным шагом h. После каждого шага вычисляется значение критерия I(x), оно сравнивается с предыдущим значением и, в случае улучшения критерия, шаги продолжаются до тех пор, пока очередной шаг не окажется неудачным. После этого поиск максимума продолжается из последней точки в обратном направлении с шагом в k раз меньше прежнего. Эта процедура поиска продолжается до тех пор, пока не будет выполнено условие:

| h | £ d,

где d – заданная погрешность определения оптимума.

1.4  Метод дихотомии

Этот метод отыскания экстремума применим для класса унимодальных функций. Идея метода проста – делить интервал [a,b], где расположен оптимум I(x), пополам

x₀ = (a + b)/2

и отбрасывать часть, где оптимума заведомо быть не может. С этой целью достаточно вычислить показатель качества I(x) в точках x₀ ± d, отстоящих друг от друга на расстояние 2d < d, где d – заданная погрешность определения оптимума. По двум вычисленным значениям I(x₀–d) и I(x₀+d), в силу унимодальности функции I(x), легко установить новый интервал неопределенности по следующим условиям (при поиске максимума):

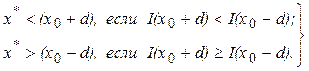                   (1.4)

Таким образом, в результате двух вычислений I(x) промежуток, где содержится оптимум, сокращается почти вдвое. Следующая пара измерений проводится в районе середины нового интервала неопределенности [a, x₀+d] или [x₀–d, b] в зависимости от того, какое из условий (4.4) выполняется.

Аналогично производятся последующие шаги поиска до тех пор, пока на k-ом шаге после 2k измерений I(x) длина интервала неопределенности l_k = (b-a)/2^k, где находится оптимум, не станет меньше или равен d, т. е. l_k£d.