Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 4

В этом случае число связей (5.14) m меньше размерности n вектора искомых переменных х_ί. Требования m<n связано с тем, что в противном случае множество допустимых решений задачи представляет собой либо набор изолированных точек, являющихся корнями системы уравнений (5.14), либо вообще пусто. При m=n, если система (5.14) совместна, может оказаться, что система (2.14) имеет единственное решение и задача оптимизации не имеет смысла.

Если ранг матрицы Якоби равен m, т.е.

,                  (2.15)

то m уравнений связи можно в простейших случаях разрешить относительно m переменных (например, х₁, х₂, …, х_m), выразив их через n-m остальных. Подстановка их в целевую функцию  приводит к задаче на безусловный экстремум функции n-m переменных. Условие (2.12) является условием регулярности типа линейной независимости для задач на условный экстремум.

Выразим х₁, х₂, …, х_m через остальные n-m переменных

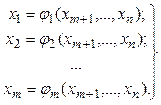                                       (2.16)

Подставляя (2.16) в (2.10), получаем задачу безусловной оптимизации без ограничений:

                            (2.17)

Решая задачу (2.17) находим  и подставляя их в (2.16), находим оптимальные значения остальных переменных: х^*₁, х^*₂, …, х^*_m

При наличии нескольких ограничений в виде нелинейных уравнений практически затруднено и даже невыполнимо решение системы (2.14) относительно m переменных с целью их выражения через остальные n-m переменных и исключение таким образом ограничивающие условия. Поэтому данный метод имеет ограниченное применение и уступает по эффективности методам Лагранжа и штрафных функций.

2.3 Метод множителей Лагранжа

Рассмотрим задачу условной оптимизации с ограничением в виде равенств

                       (2.18)

при условии

                                       (2.19)

Предположим, что условие регулярности (2.12) выполняется, т.е.

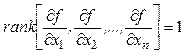
Метод множителей Лагранжа заключается в следующем: составляют вспомогательную функцию, в которую входит уравнение связей (2.19)

                        (2.20)

Функция L называется нормальной функцией Лагранжа, а коэффициент λ – неопределённым множителем Лагранжа (λ пока неизвестная величина).

Если в точке  функция  достигает максимума (или минимума) при условии (2.19), то функция  так же достигает минимума (или максимума) по х в этой точке. При этом по переменной λ функция  достигает максимума (или минимума), т.е. точка  является Седловой точкой функции .

Поэтому для решения задачи оптимизации определяем точку, в которой частные произведения равны нулю:

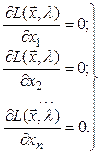                                       (2.21)

Решив систему уравнений (2.21), определяем

,                               (2.22)

зависящие от неопределённого множителя λ. Чтобы определить значение λ, найдём и приравняем нулю частную производную  по λ:

                              (2.23)

Подставим выражение (2.22) в уравнение (2.23)

                          (2.24)

Отсюда определяем λ и подставляем его в выражение (2.22), окончательно находим экстремальную точку. Подставляя  в (2.18), можно вычислить экстремальное значение критериев.

Если имеется несколько ограничений в виде равенств, то каждому из этих ограничений соответствует свой множитель λ_і Лагранжа. Так, для решения задачи

                             (2.25)

при условиях

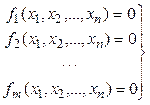,                        (2.26)

при выполнении условия 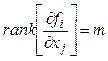 нормальная функция Лагранжа имеет вид

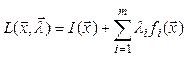                              (2.27)

Для определения условного экстремума составляем систему уравнений

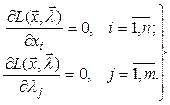                                  (2.28)

Из (m+n) уравнений (2.28) определяем n переменных ,  и m множителей λ_j , .

Если условия (2.26) таковы, что не выполняется условие регулярности (2.12), то правило множителей с нормальной функцией Лагранжа в этом случае не справедливо. Для перехода к задаче на безусловный экстремум составляют функцию Лагранжа вида

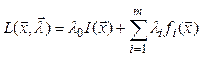,                               (2.29)

где, – неопределённые множители Лагранжа, и решают задачу таким же образом, как и при составлении нормальной функции Лагранжа.

Следует особо отметить, что метод множителей Лагранжа позволяет найти лишь необходимые условия существования условного экстремума для конкретных функций, имеющих к тому же непрерывные производные. Полученные значения, , могут и не давать экстремального значения функции, что точно так же как и в задачах на безусловный экстремум, рассмотренный выше. Поэтому найденный при решении системы уравнений (2.28) значение переменных , , должны быть проверенны на экстремум с помощью анализа производных более высокого порядка или какими либо другими методами.

Часто в примерах оптимальных задач анализ условного экстремума требует довольно сложных выкладок при исследовании высших производных. Поэтому по возможности характер найденного экстремума определяется исходя из физического смысла решаемой задачи.

2.4 Пример применения метода множителей Лагранжа

Оптимизация распределения нагрузок между параллельно работающими агрегатами.

В пищевой, химической промышленности, энергетике и других отраслях часто используются системы, состоящие из параллельно включённых объектов. Это связанно с расширением производства путём ввода дополнительных мощностей. Кроме того, при этом повышается надёжность системы, так как вывод из строя части объектов не делает её неработоспособной; при переменных нагрузках отключение части объектов позволяет оставшимся работать в более экономичном режиме.

Система из n таких параллельных объектов изображена на рис. 2.1

Сделаем два важных допущения:

1. Состав работающих объектов определён, т.е. каждый объект включён и должен потреблять сырья не менее х_{i min}.

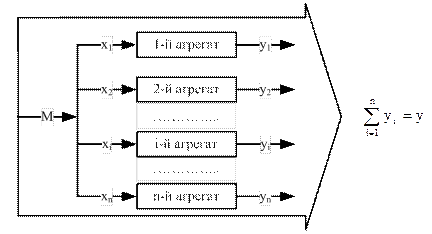
Рисунок 2.1 – система параллельных объектов

2. Нагрузочные характеристики y_i = ƒ_i(x_i) – выпуклые функции. Возможный вид такой характеристики показан на рисунке 5.2

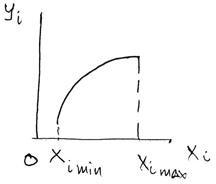
Рисунок 2.2 Нагрузочная характеристика объекта

Сформулируем задачу об оптимальном распределении нагрузок как задачу о таком выборе расходов сырья x_i на каждый объект, чтобы общая производительность у всех n объектов была максимальна при заданном расходе сырья на всю систему М. При этом будут предлагать расходы сырья скалярными величинами, т.е. не учитывать, например его состав.