Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 13

Задача линейного программирования (ЗЛП) в общем случае может быть сформулирована следующим образом.

Найти значения переменных , доставляющие минимум (максимум) целевой функции:

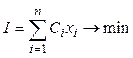                                           (4.7)

при условиях

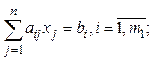                                         (4.8)

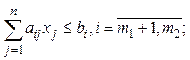                                    (4.9)

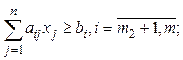                                   (4.10)

                                              (4.11)

Здесь  -заданные весовые коэффициенты целевой функции, положительные, отрицательные, среди которых могут быть также равные нулю; -переменные, которые в ЗЛП в подавляющем большинстве случаях имеют конкретный физический смысл единиц продукции, цены и т. п. и поэтому не могут быть отрицательными. Поэтому условие  также входит в систему ограничений. Коэффициенты  в ограничениях принимаются действительными числами, положительными или отрицательными, среди которых могут быть равные нулю.

Естественно, что число линейно независимых равенств  должно быть меньше числа независимых переменных. Общее же число неравенств может быть произвольным. Если ,т.е. число неизвестных равно числу уравнений (2.8) и система уравнений совместна, то она является определенной и обладает одним единственным решением. В этом случае задача оптимизации теряет смысл. В ЗЛП основной является ситуация, когда  и существуют различные решения, среди которых необходимо выбрать оптимальное решение.

4.3 Геометрическая интерпретация ЗЛП

Для простоты дальнейших рассуждений предположим вначале, что отсутствуют ограничения в форме неравенств и требуется найти максимальное значение критерия. Случай, когда требуется найти минимальное значение критерия, может быть сведен к задаче максимизации умножением на (–1 ) функции . Тогда ЗЛП может быть представлена в виде:

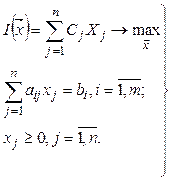                               (4.12)

Необходимое условие существования оптимального решения в ЗЛП связано с наличием системы ограничений. Из системы (4.12) видно, что при отсутствии ограничений оптимального решения не существует, так как значения переменных в целевой функции могут быть бесконечными. Система же линейных ограничений задает допустимое множество значений . Причем это множество является выпуклым многогранником в силу линейности ограничений и уравнений связи.

Дадим задаче линейного программирования геометрическую интерпретацию. Пусть число линейно независимых уравнений на два меньше числа переменных, т. е.

Любым переменным  можно придавать произвольные значения. Такие переменные называются свободными. Остальные переменные выражаются через свободные и называются базисными.

Выбрав любые две переменные, например , в качестве свободных, выразим через них остальные базисных переменных:

                     (4.13)

 по условию задачи. Выбрав значения , получим  уравнений прямых, которые на плоскости  составят границу области допустимых решений. Эта область на рис.4.1 выделена штриховкой. Стрелки указывают область решений неравенств, пересечение которых определяет область допустимых решений.

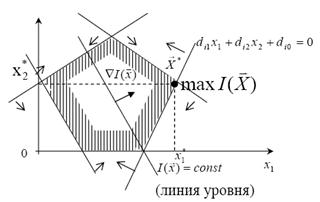
Рисунок 4.18 – Область допустимых решений

Определим теперь оптимальное решение из числа допустимых. Используя выражения (4.13), выразим  через свободные переменные  и :

                            (4.14)

Найдем такие и , при которых  достигает оптимального значения. Придавая  различные постоянные значения получим линии равного уровня в виде параллельных прямых на плоскости . Пусть при перемещении прямой  в направлении, указанном стрелкой, целевая функция будет возрастать. Очевидно, что максимального значения  достигает в наиболее удаленной точке  допустимой области. Эта точка представляет собой вершину многогранника ограничений. Подставляя в выражения (4.13) значения и , можно найти оптимальные значения базисных переменных , а из выражения (4.14) –оптимальное значение критерия .

Результатом геометрических рассмотрений задачи линейной оптимизации на плоскости являются следующие выводы, которые справедливы и в многомерной задаче:

1) для того, чтобы существовало оптимальное решение, целевая функция должна быть задана на замкнутом ограниченном множестве;

2) число линейно независимых уравнений, которые задают множество ограничений, должно быть меньше числа неизвестных переменных;

3) решение ЗЛП всегда достигается на границе области допустимых решений (многогранника ограничений);

4) область допустимых решений является выпуклым многогранником в силу линейности ограничений;

5) решение ЗЛП является единственным, если линия равного уровня целевой функции не параллельна линиям ограничений в той стороне, где достигается оптимум (решение находится в вершине многогранника ограничений, рисунок 4.1); в противном случае решение совпадает с одним из ребер (параллельным линию равного уровня в стороне оптимума, отрезок АВ на рисунке 4.2) многогранника ограничений и задача имеет бесконечное число решений, определяемых точками соответствующего ребра, причем значение  во всех этих точках решения одинаково; если область допустимых решений открытая в стороне оптимума ЗЛП не имеет решения (рисунок 4.3)

6) для того, чтобы найти оптимальное решение, достаточно перебрать вершины многогранника ограничений и выбрать из них ту, где функция  достигает оптимального значения.

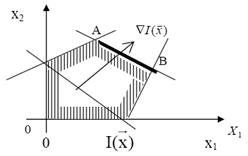
Рисунок 4.19 – Множество оптимальных решений на отрезке АВ

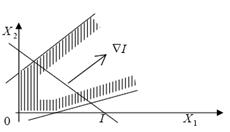
Рисунок 4.20 – Открытая область допустимых решений

4.4 Основы симплекс-метода

Рассмотрим задачу линейного программирования с условиями в форме равенств, которые задают выпуклое множество (многогранник) допустимых решений.

Прямой перебор вершин выпуклого многогранника ограничений является трудоемким способом решения ЗЛП. Поэтому разработаны и разрабатываются алгоритмы направленного поиска оптимального решения. Наиболее распространенным методом поиска является симплекс-метод (метод последовательного улучшения плана). При использовании этого метода решение задачи распадается на два этапа:

1) отыскание координат первой вершины многогранника ограничений, или, в терминах линейного программирования, опорного решения (опорного плана, базисного решения);

2) отыскание координат вершины многогранника ограничений, соответствующей оптимальному значению  (оптимального плана).