Симплекс-метод, как указывалось выше,
предполагает на первом этапе решения задачи выбор базисных переменных 
таким
образом, чтобы выполнялись условия (4.19), что является трудоемкой задачей. Для
такого выбора можно вводить дополнительные положительные переменные 
.Этот подход позволяет установить
существование допустимых решений. Однако для его реализации требуется решать
одну вспомогательную задачу линейной оптимизации тем же симплекс-методом.
Рассмотрим исходную задачу (4.15),(4.16). Для нее построим вспомогательную задачу: найти
(4.23)
для известного вектора 
с m
дополнительными переменными
и условиями
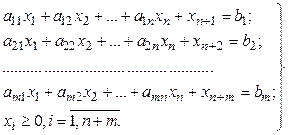(4.24)
Система уравнений (4.24) является
канонической системой. Принимая 
за свободные переменные, а -
за базисные, получаем базисное допустимое решение вспомогательной задачи:
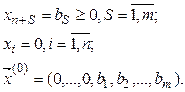
Затем, применяя последовательно шаги
симплекс-алгоритма находим оптимальное решение вспомогательной задачи. Если это
решение таково, что 
,то оно определяет допустимое базисное решение
исходной задачи; если 
, то исходная задача не
имеет допустимых решений.
Применение симплекс-метода для решения задач с условиями типа неравенство. Пусть ограничения задаются не уравнениями, а неравенствами. Их число обозначим через d. Неравенства могут быть легко сведены к уравнениям, если ввести в таком же количестве дополнительные положительные переменные. Для неравенства
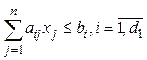
получим
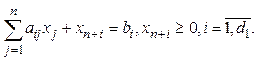
Для неравенства
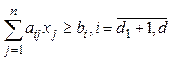
получим
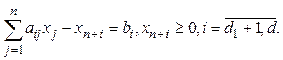
Тогда задача оптимизации может быть записана в следующей форме:
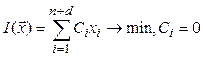при
при условиях
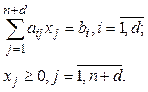
Таким образом, получили ЗЛП с условиями в форме равенств, которая решается симплекс-методом.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
1. Зайцев М.Г., Варюхин С.В. Методы оптимизации управления и принятия решений [Текст] / М.Г. Зайцев, С.В. Варюхин .-М.: ДЕЛО, 2007.-684 с.
2. Э. Хофер, Р. Лундерштедт Численные методы оптимизации [Текст] / Э. Хофер, Р. Лундерштедт .- М.:БИНОМ, 1998.-134 с.
3. П. В. Конюховский Математические методы исследования операций в эко номике [Текст] / П.В. Конюховский. - М.: ЮНИТИ, 2000.- 205 с.
4. Банди Б. Методы оптимизации. Вводный курс: Перевод с английского [Текст] / Б. Банди.– М.: Радио и связь, 1988.– 128 с.
5. Батищев Д.И. Поисковые методы оптимального проектирования [Текст] / Д.И. Батищев.– М.: ЮНИТИ, 2005.– 216 с.
6. Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии [Текст] / А.И Бояринов., В.В Кафаров.– М.: Химия, 1995.– 576 с.
7. Дегтярев Ю.И. Методы оптимизации [Текст] / Ю.И. Дегтярев.– М.: ЮНИТИ, 1998.– 272 с.
8. Куропаткин П.В. Оптимальные и адаптивные системы [Текст] / П.В. Куропаткин.– М.: Высшая школа, 2003.– 287 с.
9. Понтрягин Л.Г. Математическая теория оптимальных процессов [Текст] / Л.Г. Понтрягин.– М.: Наука, 1976.– 392 с.
10. Растригин Л.А. Системы экстремального управления [Текст] / Л.А. Растригин.– М.: Наука, 2004.– 632 с.
11. Ротач В.Я. Теория автоматического управления теплоэнергетическими процессами [Текст] / В.Я. Ротач.– М.: Энергоатомиздат, 2004.– 296с.
12. Фельдбаум А.А. Основы теории оптимальных автоматических систем [Текст] / А.А. Фельдбаум.– М.: Наука, 1986.– 624 с.
13. Цирлин А.М. Оптимальное управление технологическими процессами [Текст] / А.М. Цирлин.– М.: Энергоатомиздат, 2004.– 400 с.
14 Ефимова А.Б Сборник задач по математике. Методы оптимизации [Текст] / А.Б. Ефимова. - М.: Наука, 2003.-198 с.
СОДЕРЖАНИЕ
..................
ВВЕДЕНИЕ................................................................................................... 3
1 Методы одномерной оптимизации...................................................... 4
1.1 Одномерная оптимизация методом классического анализ...... 5
1.2 Метод равномерного поиска............................................................. 7
1.3 Метод поразрядного приближения................................................. 7
1.4 Метод дихотомии................................................................................ 8
1.5 Метод золотого сечения.................................................................... 9
1.6 Метод квадратичной интерполяции.............................................. 11
.................. 2 Методы многомерной оптимизации на основе преоб- разования задач 14
2.1 Метод классического анализа........................................................ 15
2.2 Метод исключения переменных.................................................... 17
2.3 Метод множителей Лагранжа........................................................ 18
2.4 Пример применения метода множителей Лагранжа................. 21
2.5 Метод множителей Лагранжа с ограничениями в виде не-равенства 25
2.6 Экономическая интерпретация множителей Лагранжа........... 27
2.7 Метод штрафных функций.............................................................. 29
.................. 3 Поисковые методы многомерной оптимизации............................ 33
3.1 Общие сведения................................................................................. 33
3.2 Градиентные методы оптимизации............................................... 38
3.2.1 Метод релаксации.................................................................. 38
3.2.2 Метод градиента..................................................................... 41
3.2.3 Метод наискорейшего спуска.............................................. 46
3.3 Безградиентные методы оптимизации поиска............................ 49
3.3.1 Метод сканирования.............................................................. 49
3.3.2 Метод Гаусса-Зейдел.............................................................. 51
3.3.3 Метод поиска по симплексу................................................. 54
.................. 4 Линейная оптимизация........................................................................ 62
4.1 Примеры задач линейной оптимизации....................................... 63
4.2 Общая постановка задачи линейной оптимизации.................... 65
4.3 Геометрическая интерпретация ЗЛП............................................ 66
4.4 Основы симплекс-метода................................................................ 70
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ 78
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.