Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 5

Обозначим через ƒ_i(x_i) зависимость производительности i – го объекта у_i от расхода сырья – нагрузочную характеристику. Будем считать, что эта производительность соответствует оптимальному выбору всех его режимных переменных, кроме нагрузки по сырью. Тогда задача оптимизации примет вид

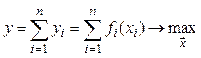                              (2.30)

при условии

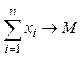 или 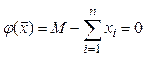                      (2.31)

.

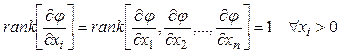Нормальная Функция Лагранжа для задачи (2.30), (2.31) принимает вид

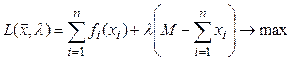                   (2.32)

Необходимые условия максимума  приводят к соотношениям

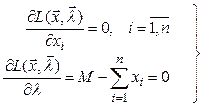                                (2.33)

Решаю систему уравнений (2.33), получаем

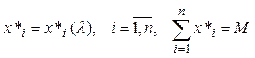
Отсюда находим λ и , .

Полученное решение  проверяется на максимум , кроме того, ни один из объектов не должен выйти на предельное значение расхода сырья, т.е. должен выполнять условие , . На практике, однако, некоторые объекты не могут работать при предельных нагрузках. Изложим алгоритм последовательного назначения предельных нагрузок, предназначенных для работы расчёта оптимального решения в этом случае.

Введём ограничения, наложенные на каждую из нагрузок,

,                                (2.34)

Будим называть нагрузки, подсчитанные из условий стационарности (2.33) функция Лагранжа без учёта ограничений (2.32) на x_i стационарными и обозначают их как .

1-й шаг. Из уравнений (2.33) рассчитываем стационарные нагрузки  без учёта (2.32) после чего разбиваем все объекты на три группы – недогруженные (), перегруженные () и средние (). Множество индексов недогруженных агрегатов обозначим через N, а перегруженных – через Р.

2-й шаг. Подсчитываем суммарную перегрузку как разницу между суммой стационарных нагрузок и предельных нагрузок для перегруженных объектов.

Аналогично рассчитываем суммарную недогрузку по всем недогруженным объектам

3-й шаг. Возможны три случая:

а) если Δ_P > Δ_N , то оптимальные нагрузки перегруженных объектов следует назначить равные предельные значениям

Найти сумму этих нагрузок , вычесть её из М и оставшуюся нагрузку (М-L₁) распределять между оставшимися объектами (выполнять шаг 1 для оставшихся объектов);

б) если Δ_P < Δ_N то оптимальные нагрузки неотгруженных объектов следует принимать минимально доступными

рассчитывать , а оставшуюся нагрузку (М-L₂) распределить между средними и перегруженными объектами (шаг 1 );

в) если Δ_P = Δ_N , то всем перегруженным объектам назначают максимальные , всем недогруженным – минимальные нагрузки , а средним – рассчитывать для них стационарные нагрузки . В этом последнем случае задача решена.

В случаях «а» и «б» переходим к шагу 1 с меньшей суммарной нагрузкой и меньшим числом объектов. Так как после каждого цикла число объектов, нагрузки которых не определены, уменьшается хотя бы на единицу, то решение будет получено после конечного числа циклов, не превышающего n.

2.5 Метод множителей Лагранжа с ограничениями

в виде неравенств

Ограничение в виде неравенств существенно усложняет решение задачи оптимизации, несмотря на то, что они уменьшают область допустимого изменение переменных. Экстремум функции может достигать не только внутри области, но и на границе области.

Необходимые условия области существования экстремума существования многих переменных с ограничениями в виде неравенств сформулированы в теории Куна-Таккера.

Рассмотрим задачу оптимизации.

                               (2.36)

при условиях

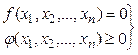.                                   (2.37)

Составим функцию Лагранжа

                  (2.38)

где λ и μ – неопределённые множители Лагранжа.

В теореме Куна-Теккера утверждается:

Чтобы точка  являлась экстремумом функции  при ограничениях вида (2.37), необходимо, чтобы она была экстремумом функции  и, кроме того, чтобы выполнялось так называемое условие дополняющей не жесткости

                                       (2.39)

Условие дополняющей не жесткости (2.39) означает, что либо неопределённый множитель μ, либо функция φ(х) должны быть равны нулю. В первом случае (если μ = 0) экстремум находится внутри области, ограниченной кривой φ(х) ≥ 0, и поэтому при решении задачи это ограничение не принимается во внимание. Во втором случае (если φ(х) = 0) решение находится на границе, поэтому ограничение в виде неравенства заменяется ограничение в виде равенства и задача решается как обычно методом неопределённых множителей Лагранжа.

Если имеется несколько ограничений в виде неравенств, то каждому из этих ограничений соответствует свой множитель Лагранжа и условие дополнительной не жесткости.

Так, для решения задачи

                                    (2.40)

При условии

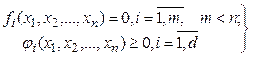                         (2.41)

функция Лагранжа имеет вид

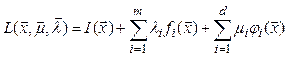                   ﴾2.42﴿

Условия дополняющие не жесткости тогда будут иметь вид

                                      ﴾2.43﴿

Необходимые условия экстремума:

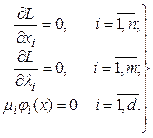                                        (2.44)

Решая системы (2.44), находим оптимальное решение задачи.

Наметим план решения задачи:

1. Сачала задаёмся μ_і = 0, i =1,d , решаем систему (2.44), определяем .

2. Проверяем выполнение неравенств (2.41). Если они выполняются, то найденное  является решением задачи.

3.Если какое-либо j – ое неравенство (или несколько неравенств) не выполняется, тогда принимаем μ ≠ 0, а φ_j﴾x﴿=0, решаем задачу с дополнительным условием φ_j﴾x﴿=0 методом множителей Лагранжа и пункты 1-3 повторяем. Эту процедуру повторяем до получения решения задачи.

2.6 Экономическая интерпретация множителей Лагранжа

В некоторых задачах Множители Лагранжа допускает экономическое толкование.

Представим себе, что условие  выражает собой ограничение на дефицит ресурса, где постоянная величина b характеризует наличие некоторого ресурса. Будем толковать функцию  как доход получаемый некоторым предприятием, при использовании ресурса.

С экономической точки зрения в этом случае множители Лагранжа интерпретируются как неявные (теневые) цены ресурсов, определяемых ограничениями. (Теневые (неявные) цены определяют приращение максимального дохода при использовании дополнительной единицы некоторого ресурса). Оптимальные значения множителей Лагранжа играет важную роль в анализе чувствительности решений. Для того чтобы пояснить эту интерпретационную схему, рассмотрим сложную оптимизационную задачу с двумя переменными и одним ограничением в виде равенства: