Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 3

где e – заданная погрешность определения экстремума, то задачу отыскания экстремума можно считать выполненной. При этом x*=x₁+Δx.

Если же условие (1.11) не соблюдается, то это означает, что исходное предположение о квадратичности целевой функции не выполняется и следует продолжать процесс поиска, то есть выполнить следующий цикл, но построение модели производить в окрестности точки x*=x₁. Эта процедура повторяется до тех пор, пока не выполнится условие (1.11).

Вполне очевидно, что критерием окончания процесса поиска экстремума может служить выполнение условия

                                        (1.15)

Таким образом, с помощью итерационной процедуры значение x^* уточняется до получения его с заданной погрешностью e.

2  Методы одномерной оптимизации на основе преобразования задач

Многие инженерные задачи связаны с оптимизацией при наличии различного вида ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой проводится поиск оптимума. Однако, несмотря на это, процесс оптимизации становится более сложным, поскольку известные критерии оптимальности решения задачи безусловной оптимизации нельзя использовать при наличии ограничений. При этом может нарушаться даже основное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым градиентом. Часто оптимум достигается в точке, не являющейся стационарной точкой функции.  Указанные трудности наталкивают на мысль использовать безусловную оптимизацию вспомогательных функций, составленных с учётом ограничений, для отыскания точки условного оптимума.

Идея преобразования задачи с ограничениями в последовательность задач без ограничений представляется эффективной в связи с наличием надёжных методов безусловной оптимизации. Это позволяет отыскать условный оптимум с приемлемой точностью путём решения относительно небольшого числа не слишком сложных задач.

Ниже рассматривается задача нелинейного программирования следующего вида:

, ,                          (2.1)

при ограничениях

, , ;                                                 (2.2)

, .                                            (2.3)

Начнём рассмотрение с краткого обсуждения метода классического анализа поиска экстремума функции многих переменных без ограничений. Этот метод часто является неотъемлемой частью методов решения преобразованной задачи оптимизации.

2.1 Метод классического анализа.

Пусть целевая функция  является непрерывной дифференцируемой функцией

                                   (2.4)

Необходимые условия экстремума:

, .                                            (2.5)

Решением этой системы уравнений определяют точки , соответствующие «подозрительным» экстремумам.

Чтобы сформировать достаточные условия рассмотрим матрицу вторых производных в точке   (матрицу Гессе)

;

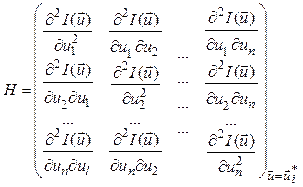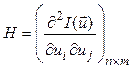                                 (2.6)

Поскольку

,

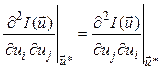матрица Гессе симметрична относительно главной диагонали.

Обозначим определители диагональных миноров матрицы (2.6) через Δ₁, Δ₂,…, Δ_n

;

;

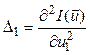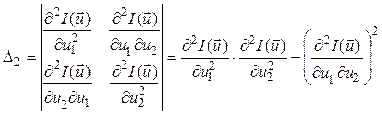и т.д.

В общем случае определитель Δ_к имеет вид:

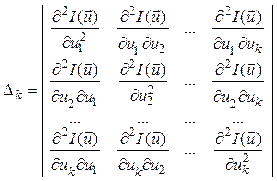                              (2.7)

Чтобы установить тип экстремума достаточно определить знаки диагональных миноров (условие Сильвестра).

В точке  функция  имеет минимум, если

, ,                                             (2.8)

или максимум, если

,.                                           (2.9)

Если же условия (2.8) и (2.9) не выполняются, но все определители Δ_к, , отличны от нуля (Δ_к ≠0, ), то в исследуемой точке  функция  не имеет экстремума. При обращении в нуль хотя бы одного из определителей Δ_к тип экстремума не определён, вопрос о наличии экстремума в исследуемой точке решается сложнее, с использованием производных более высокого порядка.

На практике обычно используют лишь необходимые условия – условия первого порядка совместно с некоторыми физическими соображениями, относящимися к конкретной задаче, ввиду сложности проверки достаточных условий – условий второго порядка.

В отдельных случаях может оказаться эффективным непосредственное вычисление  в окрестности стационарных точек, где выполняются необходимые условия.

Эффективно использовать методы исследования функции – классического анализа когда относительно просто можно найти аналитическое выражение критерия оптимальности. Применение этих методов оказывается так же полезным при предварительном анализе и более сложных задач в первоначальном, относительно грубом приближении. Поэтому эти методы не теряют своего значения в теории оптимальных процессов по мере дальнейшего его развития.

2.2 Метод исключения переменных

Рассмотрим задачу оптимизации, в которой требуется найти экстремум критерия оптимальности

                                     (2.10)

при ограничении в виде равенства

.                                       (2.11)

Экстремум, который достигается функцией  с учётом выполнения соотношения (2.11), связывающего между собой независимые переменные, называется условным или относительным в отличие от безусловного экстремума, имеющего место при отсутствии ограничений.

Поставленную задачу можно решить следующим образом. Можно решить уравнение (2.11) относительно какой-либо переменной, например х_n, выразив его через остальные n-1 переменных х₁, х₂, …, х_n-1

                                      (2.12)

Подставляя затем это выражение в (2.10), получим функцию, которая будит зависеть только от переменных х_ί, , не связанных дополнительными условиями

                                   (2.13)

Таким образом, устраняя ограничивающее условие(2.11), удалось и уменьшить размерность исходной оптимальной задачи и свести задачу с ограничениями к эквивалентной задаче безусловной оптимизации, что позволяет применить для решения методы классического анализа.

Часто имеется несколько ограничений в виде равенств

, .                                  (2.14)