Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 9

Процесс поиска продолжается до тех пор, пока , , не станут близки к нулю или пока не будет достигнута граница области задания переменных.

В алгоритме с автоматическим уточнением шага величину уточняют так, чтобы изменение направления градиента  в соседних точках  и  улучшающей последовательности составляло   (рис 3.7)

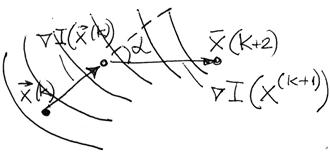
Рисунок 3.8 – Изменение направления градиента в соседних

 точках

Должно быть

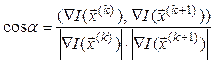
где  – скалярное произведение векторов.

;

;

;

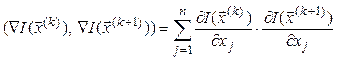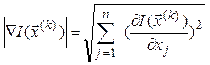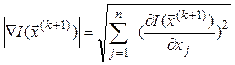Если ;

если ;

если ,

где  .

Критерии окончания поиска оптимума:

;                                      (3.14)

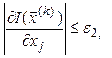,;                                 (3.15)

;                               (3.16)

;                                   (3.17)

где 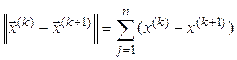 – норма вектора.

Поиск завершается при выполнении одного из условий (3.14) – (3.17).

Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции . Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек.

3.2.3  Метод наискорейшего спуска

Метод наискорейшего спуска предложен американскими специалистами Дж. Боксом и К. Уилсоном как синтез лучших свойств градиентного метода и метода релаксации.

Недостатком градиентного метода заключается в том, что на каждом шаге надо вычислять все производные функции  и определять направление градиента, что при большом числе переменных эта трудоемкая операция. Метод релаксации в том смысле обладает определенным достоинством, так как при движении вдоль выбранного осевого направления не требует вычислений производных после каждого шага. Однако в данном случае движение происходит не в оптимальном направлении, поскольку градиент в общем случае не совпадает с осевым направлением.

Метод наискорейшего спуска (крутого восхождения) сочетает основные идеи методов релаксации и градиента и заключается в следующем. Так же как в градиентном методе, в начальной точке  определяет направление градиента и перемещается в этом (при поиске максимума) или в противоположном (при поиске минимума) направлении. Однако перемещаются не на один шаг, а несколько шагов (как в методе релаксации). После каждого шага оценивается только величина критерия , производные не вычисляются (рис. 3.8)

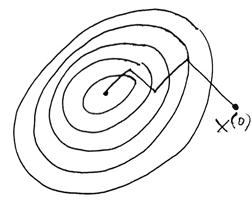
Рисунок 3.9 – Траектория движения к оптимуму в методе наискорейшего спуска

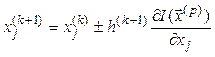, ,                 (3.18)

где  – вектор точки, в которой последний раз вычислялся градиент .

В алгоритме (3.18) знак “+” – принимается при поиске максимума, а знак “-” – при поиске минимума. В направлении градиента  выполняют шаги пока выполняется условие (при поиске минимума)

                                  (3.19)

При нарушении условия (3.19) в последней точке определяют новое направление градиента и процедуру поиска повторяют.

Критерием окончания поиска может служить одно из условий (6,14) – (6,17) градиентного спуска.

Рассмотрим возможность улучшения алгоритма поиска Итерационный поиск (6.18) в векторной форме в точке  имеет вид

                           (3.20)

С учетом этого можно определить значение  в точке :

                       (3.21)

Поскольку  и  определены, то значение целевой функции  в следующей точке

оказывается функцией только одного параметра – шага спуска (рис. 6.9). Применяя какой-нибудь метод однометрической оптимизации определяем величину оптимального шага

и координаты новой точки

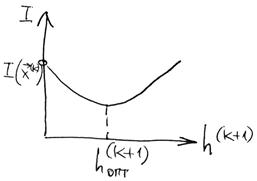
Рисунок 3.10 – Характер зависимости целевой функции от величины  шага поиска

Аналогично находим:

Вычислив в новой точке  градиент , имеем

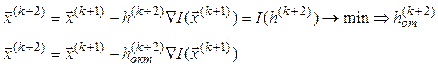
Эта процедура повторяется до выполнения одного из условий (3.14) – (3.17)

Заметим, что центральным звеном рассматриваемого алгоритма является поиск минимума функции одной переменной, что существенно увеличивает быстродействие алгоритма поиска оптимума методом наискорейшего спуска.

Этот метод, также как и другие методы градиентного спуска, определяет локальный минимум функции . Это связано с зависимостью всего пути спуска . Для определения других локальных минимумов необходимо производить поиск из других начальных точек.

3.3. Безградиентные методы оптимизации поиска

До сих пор рассматривались методы поиска оптимума, в которых производился предварительный анализ производных функций цели  по всем независимым переменным для определения направления и величины шага поиска. Это связано с необходимостью выполнения большого объёма вычислений, что приводит к увеличению времени поиска.

Кроме того, при оптимизации объекта в условиях отсутствия его математического описания, погрешность вычисления производной как разности значений и критерия оптимальности может достигать до сотен процентов из-за неизбежных погрешностей при измерений величин, характеризующих этот критерий. Причём это может иметь место даже при небольшой относительной погрешности вычислений значения критерия оптимальности. Это может привести к существенным ошибкам в определении направления движения к оптимуму с помощью градиентных методов.

Существует другая группа методов – безградиентные методы, использующие в процессе поиска информацию, получаемую не при анализе производных, а от сравнительной оценки критерия оптимальности в результате выполнения очередного шага. К ним относятся методы сканирования, покоординатного спуска (Гаусса- Зейделя), симплекса.

3.3.1 Метод сканирования

Идея алгоритма перебора крайне проста. Вычисляют значения функции  в конечном числе точек  области D_x (в узлах координатной сетки).Из вычисленных значений выбирают наименьшее (наибольшее) . Координаты соответствующего узла сетки  – это координаты экстремума, определённые с точностью до , где – h шаг сетки (рис. 6.10).

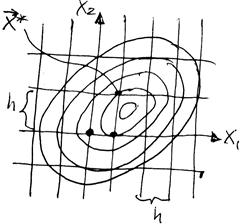
Рисунок 3.11 – Поиск оптимума на сетке переменных

Точность определения точки минимума, причем глобального, зависит от плотности наполнения области D_x дискретным множеством , то есть от величины шага h координатной сетки, тем выше точность определения положения оптимума, однако при уменьшении h быстро растёт объём вычислений. Если интервал изменения каждой переменной разбить К равных частей, то h равно

,

При этом необходимое количество вычислений I(x) равно .