2) невысокий уровень требований к объёму памяти ЭВМ, массив данных имеет размерность (n+1, n+2);
3) алгоритм оказывается
эффективным даже в тех случаях, когда ошибка вычислений ![]() велика,
поскольку при его реализации оперируют наибольшими значениями
велика,
поскольку при его реализации оперируют наибольшими значениями ![]() в вершинах, а не наименьшими.
в вершинах, а не наименьшими.
Перечисленные методы характеризуют метод поиска по симплексу как весьма полезный при проведении вычислений в реальном времени (анализ в динамике).
Недостатком метода является возможность возникновения трудностей, связанных с масштабированием, поскольку все координаты вершин симплекса зависят от одного и того же масштабного множителя альфа. Чтобы обойти трудности такого рода следует промасштабировать все переменные с тем, чтобы их значения были сравнимыми по величине.
4 Линейная оптимизация
Рассмотрим задачи, которые в математической литературе обычно называют линейным программированием, хотя термин «линейное программирование», появившийся до широкого использования ЭВМ, не соответствует современному пониманию смысла программирования.
Приведем краткую историческую справку.
В 1939 г. к Ленинградскому математику, позже академику, Л.Канторовичу обратились представители треста, выпускающего фанеру, с просьбой решить одну сугубо производственную задачу. Эта задача имела весьма локальный характер, а именно: как наилучшим образом распределить работу между станками? Дело в том что, такого рода производственные задачи имеют всегда целый ряд конкретных ограничений, с которыми вынужден считаться человек, взявшийся решать их.
Любое производство располагают ограниченными ресурсами. На заводе или цехе работает определенное количество людей, станков. Производительность станков также ограничена. Как и количество сырья, поступающего на переработку, как и многие другие ресурсы. В этих условиях требуется найти наилучший с позиций экономики способ ведения работ.
Решая такую локальную задачу, Канторович вывел определенные закономерности и создал новый метод, оказавшийся универсальным, который можно успешно применять, решая практически любую хозяйственную задачу.
Этот метод, созданный выдающимся советским ученым, получил название метода линейного программирования и широко используется в мировой практике. К нему прибегают, решая обширный класс хозяйственных задач, начиная с оптимизации грузопотоков и кончая разработкой перспективных планов для целых отраслей производства.
Новаторский научный поиск и открытие линейного программирования Л.В.Канторовичем отмечены Нобелевской премией по экономике за 1975 год.
Таким образом, линейное программирование возникло в связи с рассмотрением вопросов о нахождении наивыгоднейших вариантов при решении различных планово-производственных задач. В этих задачах имеется большая свобода изменения различных параметров и ряд ограничивающих условий. Требуется найти такие значения параметров, которые с некоторой точки зрения были бы наилучшими.
К таким задачам относятся задачи нахождения наиболее рационального способа использования ресурсов (сырья, материалов, финансов и т. д.), определения наивыгоднейших производственных режимов, оптимального распределения выпуска продукции по предприятиям, повышения эффективности работы транспорта (транспортная задача), составления рецептуры изготовления многокомпонентной смеси и т. п.
При автоматическом управлении производственным процессом эти задачи должны решаться автоматически и непрерывно. Поэтому знание методов решения подобных задач, необходимое для всякого инженера, для специалиста по информатике и автоматическому управлению становится особенно важным.
4.1 Примеры задач линейной оптимизации
Транспортная задача. Имеется n
поставщиков, производителей k видов продукции. Возможность каждого поставщика
характеризуется вектором ![]()
![]() , где
, где ![]() - количество
- количество ![]() -го
вида продукции, производимое
-го
вида продукции, производимое ![]() -м поставщиком.
Вся производимая продукция распределяется
-м поставщиком.
Вся производимая продукция распределяется ![]() потребителям
(заказчикам). Каждый потребитель характеризуется вектором
потребителям
(заказчикам). Каждый потребитель характеризуется вектором![]()
![]() ,
где
,
где ![]() - количество
- количество ![]() -го
вида продукции, производимое
-го
вида продукции, производимое ![]() -м заказчиком.
Пусть все, что производится поставщиками, потребляется заказчиками. Тогда
необходимо выполнение условия
-м заказчиком.
Пусть все, что производится поставщиками, потребляется заказчиками. Тогда
необходимо выполнение условия
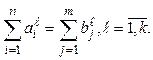 (4.1)
(4.1)
Между поставщиками и потребителями существует транспортная сеть, затраты на перевозки которой характеризуется матрицей стоимости
![]()
где ![]() – стоимость
перевозки единицы веса продукции от i-го поставщика к
– стоимость
перевозки единицы веса продукции от i-го поставщика к ![]() -му
заказчику.
-му
заказчику.
Необходимо синтезировать план перевозок по каждому виду продукции:
![]()
где ![]() - количество
- количество ![]() -го вида продукции, перевозимое от i-го
поставщика к j-му потребителю.
-го вида продукции, перевозимое от i-го
поставщика к j-му потребителю.
Этот план должен минимизировать транспортные затраты:
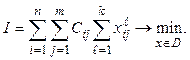 (4.2)
(4.2)
Множество D допустимых решений увязывает количество отправленных и полученных грузов. С учетом условия (4.1) имеем следующие ограничения (множество D):
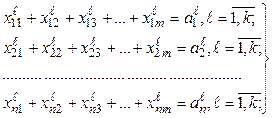 (4.3)
(4.3)
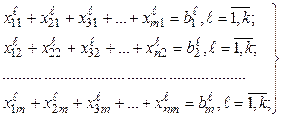 (4.4)
(4.4)
![]() (4.5)
(4.5)
Таким образом, получены ![]() ограничений в форме равенств (4.3),
(4.4) и
ограничений в форме равенств (4.3),
(4.4) и ![]() ограничений в форме неравенств
(4.5).
ограничений в форме неравенств
(4.5).
Эти ограничения можно представить в более компактной форме:
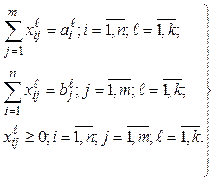 (4.6)
(4.6)
Размерность неизвестного
вектора ![]() в данной задаче равна
в данной задаче равна ![]() .
.
Таким образом получили линейную целевую функцию (4.2), линейные ограничения (4.6) и, следовательно, задачу линейного программирования.
Задача об оптимальном планировании выпуска продукции. Данная задача об определении максимальной прибыли производства является типичной задачей линейной оптимизации.
Пусть для изготовления n
видов продукции в количестве ![]() расходуется m
видов сырья. Расход сырья i-го вида на единицу j-го вида продукции равен
расходуется m
видов сырья. Расход сырья i-го вида на единицу j-го вида продукции равен ![]() , запас сырья i-го вида ограничен
величиной
, запас сырья i-го вида ограничен
величиной ![]() . Каждая единица продукции i-го вида
дает прибыль
. Каждая единица продукции i-го вида
дает прибыль ![]() рублей.
Задача поиска вектора
рублей.
Задача поиска вектора ![]() – количества продукции
каждого вида, дающего максимальную прибыль, принимает следующую форму: найти
– количества продукции
каждого вида, дающего максимальную прибыль, принимает следующую форму: найти ![]() , доставляющий
, доставляющий
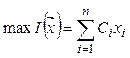
при ограничениях
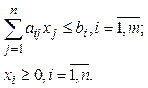
В приведенных выше задачах, а также в ряде других задач, целевая функция линейно зависит от переменных. Если и ограничения на переменные и уравнения связи при этом линейны, то такие задачи составляют предмет линейного программирования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.