Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 6

                                   (2.45)

при ограничении

                                         (2.46)

Функция Лагранжа имеет вид

Необходимые условия оптимума следующие:

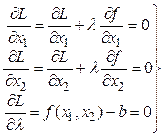                                    (2.47)

Из этой системы уравнений находим оптимальные значения x₁,х₂, λ.

Пусть λ* – оптимальное значение множителя Лагранжа, а ,  – оптимальное решение задачи. Далее, пусть максимум функции  при λ = λ* достигается в точке , причём  и . Очевидно, что оптимальные значения  связаны функциональной зависимостью с величиной b, задающей границу наличия дефицитного ресурса.

Изменения I* (оптимального значения I), обусловленные изменениями b , описываются частной производной . По правилу дифференцирования сложной функции имеем:

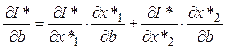                         (2.48)

Дифференцируя обе части ограничения f﴾x₁, х₂) – b=0, получаем

                         (2.49)

Умножим обе части равенства (2.49) на λ* и суммируем с равенством (2.48):

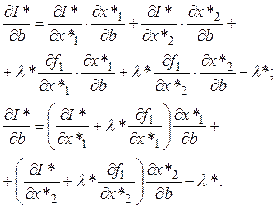                   (2.50)

Так как  и λ* удовлетворяют уравнениям (2.47), равенство (2.20) приводится к виду

                                              (2.51)

Таким образом, из формулы (2.51) следует скорость изменения оптимального значения I, вызываемого изменением b, с точностью до знака равна оптимальному значению множителя Лагранжа (на знак самого множителя Лагранжа λ никаких требований не накладывается). Другими словами, величина изменения оптимального значения целевой функции (теневая цена), обусловленного единичным увеличением правой части ограничения, задаётся множителем Лагранжа. В зависимости от знака λ* значение I* при изменении b могут увеличиваться или уменьшатся.

В случае когда рассматривается оптимизационная задача с m ограничениями и n переменными (m<n):

при ограничениях

пользуясь аналогичной схемой рассуждений, можно показать, что

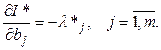
2.7 Метод штрафных функций

Рассмотрим решение задачи условной оптимизации

                           (2.52)

при

                        (2.53)

метод штрафных функций заключается в безусловной минимизации обобщенной целевой функции

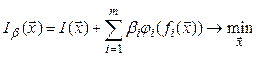                     (2.54)

где ,  – коэффициенты штрафа;

       ,  – штрафные функции.

В отличии от множителей Лагранжа коэффициенты штрафа задаются: . Обычно .

Функции штрафа должны удовлетворять условию

,

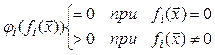При решении задач оптимизации широко используется квадратичные и модульные штрафы:

 

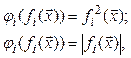
С помощью штрафной функции исходная задача (2.52), (2.23) условной минимизации преобразуется в последовательность задач безусловной минимизации функции (2.54). Эта задача решается численными методами, но условия оптимальности классического анализа могут быть использованы и здесь:

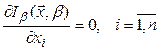
Решение этой системы даёт , .

В общем случае невозможно аналитически определить положение минимума функции , рассматривая её как обычную функцию от от β. Для его определения необходимо обратится к численным методам.

При  решение задачи безусловной минимизации стремится к решению  задачи нелинейного программирования:

,

Наряду с этими многочисленными исследованиями доказано, что обязательным следствием неограниченного увеличения штрафного параметра β является плохая обусловленность подзадач безусловной минимизации, проявляющаяся в сильной деформации соответствующих поверхностей уровня.

Поэтому для того, чтобы можно было применить настоящий метод на практике, необходимо построить вычислительный алгоритм, использующий теоретическое свойство сходимости последовательности оптимальных решений подзадач безусловной оптимизации к оптимальному решению , , задачи с ограничениями. Теоретически здесь не возникает трудностей. Необходимо выбрать начальное значение β = β⁽⁰⁾, что бы сформировать функцию , которая минимизируется без ограничений численными методами. Найдя минимум функции , необходимо увеличить значение β. Это можно сделать просто, если найти , где константа с>1, однако выбор с произволен, удачным могут быть различные значения С в зависимости от свойств функции  и ограничений . Затем необходимо минимизировать функцию , снова используя численный метод. Таким образом, будет заработана итерационная процедура. На каждом шаге минимизируется функция , минимум которой находится в точке . Важно, что её можно использовать в дальнейшем в качестве начальной точки в итерационной процедуре минимизации функции , где β^(к+1) = с β^(к)

Теперь ясно, что последовательность β^(к) возрастает и стремиться к бесконечности, следовательно, последовательность точек минимумов  безусловной минимизации будет сходиться к решению исходной задачи с ограничениями .

Выбор начального значения β⁽⁰⁾ может оказаться важным с точки зрения сокращения числа итераций при минимизации функции . Если сначала β⁽⁰⁾ выбрано очень малым, для того чтобы функция  мало отличалась от функции , то метод будет сходится очень быстро. Однако такой выбор может привести к серьёзным осложнениям при вычислениях. Для малых β функция  будет быстро меняться в окрестности минимума, что может вызвать затруднения при использовании градиентных методов. Слишком же большое значение β может привести к тому, что штрафная функция

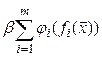
в выражении (2.24) станет доминирующей. Поэтому разумный выбор начальной точки β⁽⁰⁾ очень важен. Для многих задач разумным значением для начальной точки является значение β⁽⁰⁾ =1.

Для уменьшения влияния произвола в выборе коэффициента штрафа применяют метод последовательной безусловной минимизации (МПБМ) Мак-Кормика и Фиакко, состоящий обобщенной функции Iβ ﴾x,β﴿ с увеличивающимся штрафом:

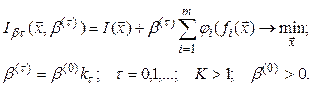
при этом оптимальное значение  используют как начальную точку на -ом цикле минимизации. Обычно берут k = 4-2, β₀ = 1 и заканчивают поиск, когда решение  мало отличается от предыдущего решения  на предыдущем цикле.

Метод штрафных функций приводит задачу условной оптимизации той же размерности, что и исходная, в отличие от метода Лагранжа. Метод легко алгоритмизируется для ЭВМ, но требует опыта выбора коэффициентов штрафа и даёт отлично невысокую точность; находит наибольшие применение при численном решении задач на ЭВМ.

3 Поисковые методы одномерной оптимизации

3.1 Общие сведения