Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 10

Поэтому эффективное применение данного метода ограничивается задачами невысокой размерности (n=2-3). При большой размерности вектора  требуется выполнение большого объёма вычислительной работы.

Пусть область D_x – геперкуб:

,

в котором ищется .Точность определения координат вектора , минимизирующего , положим равной 0,1. Тогда интервалы  следует разбить на 10 частей с шагом h=0,1 плоскостями, ортогональными  и вычислить во всех точках перечисления плоскостей значения . Всего потребуется вычислить  в 11ⁿ точках. Пусть для нахождения I в каждой точке требуется примерно 10²n арифметических операций. Тогда общее число арифметических операций алгоритма перебора примерно 11⁽ⁿ⁺²⁾n и при n=10 на ЭВМ с быстродействием 10⁹ oп/c требуется примерно 10⁴ с, т.е. примерно 167 минут непрерывной работы ЭВМ.

Иногда поиск осуществляется с переменным шагом сканирования. Вначале величина h выбирается достаточно большой, выполняется грубый поиск для локализации экстремума, а поиск в районе оптимума осуществляется с меньшим шагом.

Достоинства метода – возможность определения глобального оптимума и независимость поиска от вида оптимизируемой функции.

3.3.2 Метод Гаусса-Зейделя

Метод Гаусса-Зейделя, называемый также методом покоординатного спуска, аналогичен методу релаксации. Отличие заключается лишь в том что, в этом методе не определяется осевое направление, вдоль которого значение  изменяется наиболее сильно. Поочерёдно изменяются все переменные.

Алгоритм поиска минимума следующий. Пусть ищется минимум . Устанавливается очерёдность изменения  –  и начальная точка  поиска. Затем все переменные  фиксируются на уровне ,  изменяется по алгоритму

; ; ;        (3.22)

где  – шаг изменяется , обычно  не зависит от k.

После каждого шага вычисляется , сравнивается с предыдущим значением, критерия шаги продолжаются до достижения частного оптимума по x_j = x₁. В этой точке величина  фиксируется и изменяется x₂ до достижения оптимума по x₂ и т.д. После того как достигается оптимум по последней переменной x_n, снова изменяется x₁ и весь цикл повторяется до тех пор, пока не будет найдена точка оптимума.

На рисунке 3.11 показан алгоритм поиска минимума для функции двух переменных.

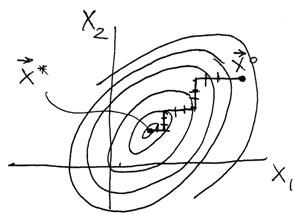
Рисунок 3.12 – Траектория движения к оптимуму в методе координатного спуска

Заметим что для функции двух переменных методы релаксации и Гаусса-Зейделя совпадают.

Если первый шаг изменения x_j не улучшает значение критерия, т.е. , а , то выполняется шаг по x_j в обратном направлении , т. е. Первый шаг пробный. Если и этот шаг неудачный, то переходят к изменению x_j+1 и т.д.

Поиск заканчивают когда достигается точка , из которой при движении в любом осевом направлении улучшение критерия  не наблюдается.

Рассмотрим вопрос улучшения алгоритма поиска .

Пусть в области допустимых решений D задано нулевое приближение .

Рассматриваем функцию  при фиксированных значениях  как функцию одной переменной x₁, т. е.

              (3.23)

Минимизируя  находим значение , доставляющее минимум функцию (3.23):

;

.

Далее при фиксированных значениях  рассматриваем  как функцию одной переменной x₂. Находим её минимум

;

.

Продолжая эту процедуру последовательно, после n шагов получаем точку , в которой выполняется условие

.

В результате одного шага покоординатного спуска происходит переход из начальной точки  в точку . Если при этом оказывается, что

,

то начальная точка  – точка, доставляющая минимум функцию .

Если ,то выполняется следующий шаг поко-ординатного спуска, в котором за начальную точку принимается , получаем  и т.д. Этот процесс продолжается до тех пор, пока не выполнится какое-либо условие окончания поиска, например такое

,                          (3.24)

где  – заданная точность.

или

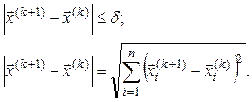               (3.25)

Таким образом, поиск минимума функции одной переменной занимает центральное место в рассматриваемом алгоритме покоординатного спуска.

Простота метода и сравнительно небольшой объём вычислений обусловили его распространение в автоматических системах поиска.

3.3.3 Метод поиска по симплексу

Рассмотрим задачу

                        (3.26)

Симплексный метод является безградиентным методом, реализует процедуру прямого поиска оптимума на основе вычисления значения целевой функции. Предполагается, что  непрерывна, а  может как существовать, так и не существовать, поскольку соответствующие числовые значения не используются. Однако следует отметить, что симплексный метод можно применить для решения задач, в которых  существует, но представляет собой сложную векторную функцию управляемых переменных. Наконец, предполагается, что функция  унимодальна в рассматриваемой области. Если же метод применяется для анализа мультимодальных функций, то приходится ограничиваться идентификацией локальных оптимумов.

Симплексный метод относится к категории эвристических, которые реализуют процедуры поиска с помощью интуитивных геометрических представлений.

Первые попытки решения оптимизационных без ограничений на основе прямого поиска связаны с использованием процедуры сканирования, что является непригодной для решения задач с числом переменных превышающим 2.

Более полезная идея заключается в выборе базовой точки и оценивания значений  в точках, окружающих базовую точку. Например, при решении задач с двумя переменными можно воспользоваться квадратным образцом (рис. 3.12), который является частным случаем кубического образца. В вершинах образца и базовой точке вычисляется значение .

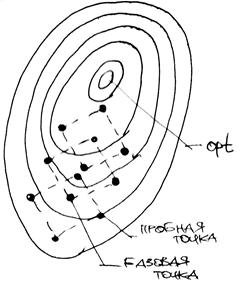
Рисунок 3.13 – Использование квадратного образца для поиска оптимума

Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск.

Этот тип эволюционной оптимизации был использован Боксом и другими исследователями США для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой.