Задача 43
Из имеющихся двух видов материала М1, М2 нужно составить такой многокомпонентный новый материал, в котором обеспечивается потребное количество компонентов A, B, C, D при минимальных затратах, если учесть, что единица количества М2 в 1,5 раза дороже единицы количества М1. Исходные данные приведены в талице
|
Компоненты |
Кол. в 1 кг М |
Потребное количество в потребном материале |
|
|
М1 |
М2 |
||
|
A B C D |
6 1 1 5 |
2 6 3 3 |
|
|
План |
|
|
|
Решение:
Пусть a – стоимость 1 кг М1.
Тогда:
![]()
При условиях:
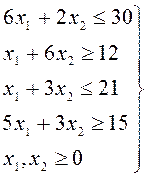
![]()
Уравнения границ области допустимых решений:
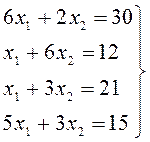
![]()
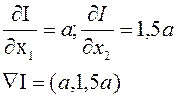
Оптимальному решению соответствует крайняя точка в направлении антиградиента. Эта точка соответствует решению уравнений:
![]() и
и ![]() :
:
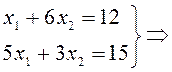
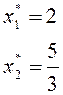
![]()
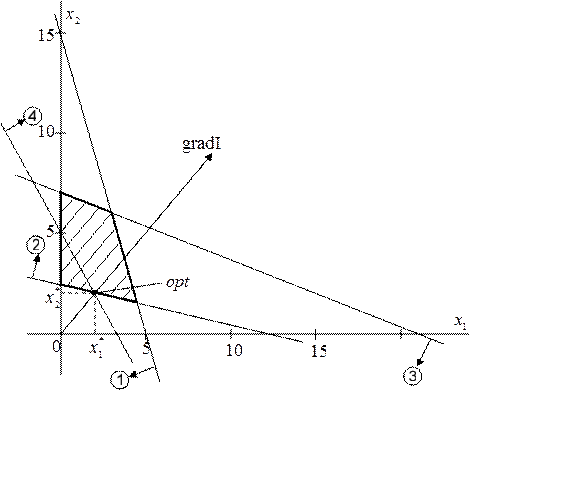
Решение симплексным методом (составление многокомплектного материала)
![]()
![]()
при:
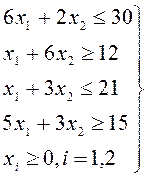
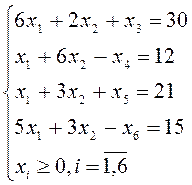
![]()
Пусть ![]() –
свободные переменные
–
свободные переменные
![]() – базисные переменные
– базисные переменные
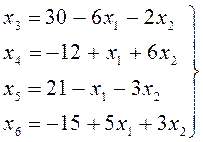
Первое базисное решение:
![]()
![]()
Решение ![]() не
допустимо, т.к.
не
допустимо, т.к. ![]() . Следовательно,
. Следовательно, ![]() не могут быть базисными переменными.
не могут быть базисными переменными.
Пусть ![]() –
свободные переменные
–
свободные переменные
![]() –
базисные переменные
–
базисные переменные
Выразим базисные переменные через свободные
Из (2) и (4):
(4)x2-(2):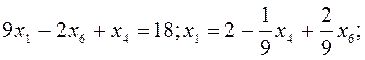
(2)x5-(4):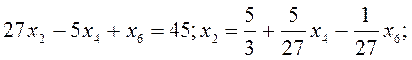
Из (1): 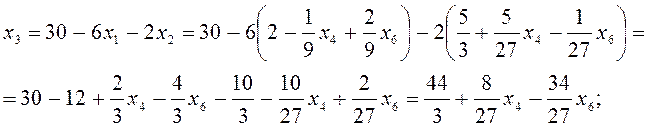
Из (3): 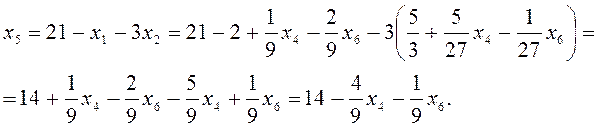
В результате имеем:
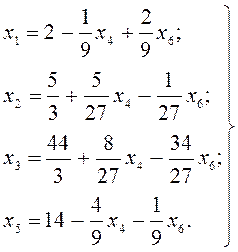
Новые базисные переменные:
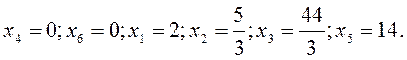
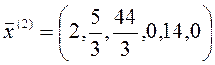
Новые свободные переменные: ![]() .
.
Выразим ![]() через
через
![]() .
.
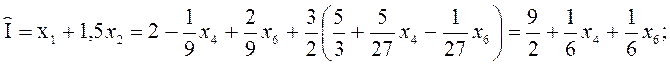
Т.к. коэффициенты при ![]() положительные, базисное решение
положительные, базисное решение ![]() оптимальное
оптимальное
Следовательно:
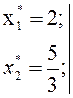
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.