В первой строке указывается остаток составов, переходящий с предыдущих суток на начало первого расчетного интервала. Во второй графе против соответствующих расчетных интервалов делаются пометки, что в течение этих интервалов горка не может быть использована для роспуска, например, по причинам смены бригад, техосмотра и ремонта горочных устройств, формирования поездов на горке.
В графе 3 из графика исполненной работы проставляется число поездов, прибывших в расформирование за каждый расчетный интервал. Графы 4 и 5 заполняются в процессе выполнения расчетов путем решения уравнения баланса.
Поскольку за каждый расчетный интервал с горки распускается один состав, в графе 5 проставляется значение, на единицу меньшее, чем в графе 4, кроме случаев, когда в графе 2 стоит особая отметка, означающая, что в данном интервале роспуск невозможен.
Средний простой составов в парке определяется:
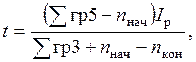
где ∑гр5 – итог числителей графы 5; ∑грЗ – число составов, прошедших через парк за сутки, без учета угловых и местных передач; Iр – расчетный интервал вывода составов из парка, мин; nнач, кон – соответственно переходящие остатки составов на начало и конец суток.
Для примера (см. табл. 10.1)
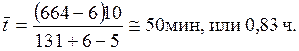
Аналогично выполняется расчет для других подсистем, затем результаты суммируются и получается общий простой для станции (сортировочной системы).
Трудоемкость расчетов (с помощью табличного моделирования) сокращена по сравнению с графической моделью при той же трудоемкости подготовки исходных данных, однако точность расчета показателей по табличному моделированию ниже: не учитывается занятость путей, работа локомотивов, враждебность в горловинах и др. Кроме того, нарушаются требования системного подхода – каждая подсистема рассматривается в качестве независимо функционирующей обслуживающей системы. Поэтому достоверность результатов, полученных табличным моделированием, часто оказывается невысокой.
Можно выделить два направления создания аналитических методов расчета простоя вагонов на станциях. Первое – на основе использования математического аппарата теории массового обслуживания (ТМО) и второе – с использованием аналитическо-статистических зависимостей. Во всех случаях аналитические зависимости используются для определения среднего времени нахождения вагона в каждой подсистеме. В связи со сложностью технологических линий и значительным числом фаз обслуживания аналитические методы также не учитывают влияние подсистем друг на друга.
Для расчетов показателей станций проф. Н. Н. Шабалин предложил определять время ожидания обслуживания (обработки, расформирования, формирования и т. д.) на основе ТМО по формуле
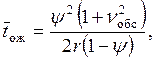
где Ψ – коэффициент загрузки
выходного канала; 
– коэффициент вариации времени обслуживания;
r – среднечасовая интенсивность поступления поездов (составов).
Эта формула получена исходя из предположения, что входящий транспортный поток является простейшим.
Пример. Требуется определить
простой составов
в ожидании расформирования, если r =
3,75 поездо-ч, Ψ = 0,75, 
= 0,9:
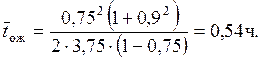
Использование предложенной проф. Н. Н. Шабалиным методики для практических целей показало, что приемлемые результаты получаются при уровнях загрузки выходного канала до 0,65–0,7. При больших значениях Ψ результаты расчетов отклоняются от реальных в сторону увеличения, превосходя фактические в несколько раз.
Аналогичные методики разработаны профессорами А. М. Акулиничевым, А. В. Быкодоровым, И. Б. Сотниковым на основе распределения интервалов входящего потока по закону Эрланга. Так, например, проф. А. М. Акулиничев среднее время ожидания обслуживания в подсистеме станции определяет:
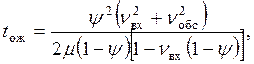
где 
– коэффициент
вариации входящего потока; μ – интенсивность обслуживания, поездов/ч.
Пример. Для исходных данных предыдущего примера рассчитать
простои в ожидании, если коэффициент вариации входного потока =0,8:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.