но команда Ii не находится в регистре команд перед циклом Т + 1. Таким образом, даже если мы обеспечиваем дополнительный сумматор для вычисления адреса перехода на этапе decode, PCi не может быть вычислен перед циклом Т + 1. Следовательно, команда Ii+1 может быть выбрана только в цикле T + 2.
Путь решения этой проблемы очень груб: изменение семантики инструкций ветвления с помощью двух правил, гласящих:
1. Ветвление, принятое в команде Ii , влияет только на PC вычисленный в следующей команде, т.е. PCi+1. Этот механизм называется delayedbranch (задержанное ветвление).
2. Если Ii является управляющей операцией, тогда команда Ii+1 следующая за Ii называется командой в слоте задержки (delayslot) Ii. Управляющие операции не допускаются в слотах задержки.
Формальное индуктивное определение механизма задержанных ветвлений
|
|
Видно, что определение адреса перехода PC + 4 + immвместо гораздо более очевидного адреса перехода PC + immмотивируется механизмом задержки ветвления. После управляющей операции Ii всегда выполняется команда IM[PCi-1+ 4] в слоте задержки Ii (потому что Ii не занимает слот задержки и, следовательно, bjtakeni-1 = 0). При адресе перехода PC + imm, может быть придется использовать вычисление
PCi+1 = PCi + immi+1 - 4
вместо
PCi+1 = PCi + immi+1.
Семантика задержки ветвления используется, например, в наборе команд MIPS [KH92], SPARC [SPA92] и PA-RISC [Hew94].
Семантика Задержанного PC
Вместо задержки принятых ветвлений можно применить задержку всех вычислений PC. Программный счетчик PC' обновляется согласно простой последовательности семантик:
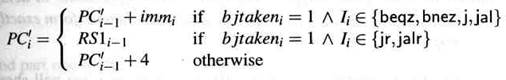
Результат просто синхронизируется с задержанным программным счетчиком DPC:
DPCi+1= pc'i .
Задержанный программный счетчик DPCиспользуется для выборки команд из IM, а именно Ii = IM[DPCi-1]. Вычисления начинаются с
PC'-1 = 4 DPC-1 = 0
Мы называем это униформой и просто осуществляем механизм задержки PC. Эти два механизма, как окажется позже, полностью эквивалентны.
Команды перехода (Jump) и связи (Link)
Мы продолжаем нашу дискуссию тонким наблюдением относительно семантики команд перехода и связи (jal, jalr) которые обычно используют для вызова процедур. Их семантика также изменяется механизмом задержки ветвлений! Сохранение PC + 4 в GPR[31] приводит к возврату в слот задержки команд перехода и связи. Конечно, возврат должен быть к
команде после слота задержки (например, смотри MIPS architecture manual [KH92]). Формально, если Ii = IM(PCi-1) команда перехода или связи, тогда
PCi = PCi-1 + 4
потому что Ii не находится в слоте задержки а команда
Ii+l=IM(PCi)
является командой в слоте задержки Ii. Команда перехода и связи Ii поэтому должна сохранить
GPR[31]i = PCi + 4 = PCi-1 + 8.
В простейшем механизме задержки PC просто сохраняем GPR[31]i = PC'i-1+4.
Эквивалентность задержанных ветвлений и задержанного PC
Теорема 4.1 > Предположим, что машина с задержкой ветвлений и машина с задержкой PC начинают работу с одной и той же программой (без управляющих операций в слотах задержки) и с одинаковыми входными данными. Обе машины выполняют одну и ту же последовательность команд I0, I1, ....
ДОКАЗАТЕЛЬСТВО Фактически это теорема моделирования. Индукцией по i мы покажем две вещи, а именно
1. (PCi , PCi+1) = (DPCi , PC'i),
2. если Ii является командой перехода или связи, тогда значение GPR[31], сохраняемое в регистре 31 в течении команды Ii одинаково для обоих машин.
Так как bjtaken-1 = 0, из этого следует, что PC0 = 4. Таким образом
(PC-1,PC0) = (0,4) = (DРС-1, РС'-1),
и первая часть и индукционной гипотезы верна для i = - 1 .
В шаге индукции мы заключаем от i — 1 до i, основываясь на индукционной гипотезе, что (PCi-1 , PCi) = (DPCi-1 , PC'i-1). Так как
DPCi = PC'i-1по определению DPC
= PCi по индукционной гипотезе,
остается только показать, что
PCi+1=PC'i,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.