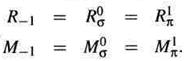
Обратите внимание, что для оставшихся регистров мы не делаем никаких предположений. Это станет критично, когда мы будем обрабатывать прерывания. Механизм, реализующий переход к процедуре обработки прерываний (JISR), почти идентичен представленному механизму сброса.
Спецификация для выполнения команд Ii машиной DLXπопределена как
IП(k,T) = i <-> T = k + i.
Теперь стратегия доказательства правильности легко описывается. Мы рассматриваем цикл Т машины DLXπи соответствующий цикл T' машины DLXσ , когда одна и та же команда, скажем Ii , находится на одном и том же этапе, скажем k. Формально
|
|
Тогда мы хотим заключить индукцией по Т что этап kмоделируемой машины в цикле Т имеет те же самые входы, что и этап kмоделирующей машины в цикле T'. Так как этапы идентичны, мы хотим заключить, что для всех сигналов s внутри этапов
|
|
Это в особенности должно быть верным для сигналов, которые синхронизируются в выходные регистры R€ out (k) этапа kв конце такта T. Это позволило бы нам заключить для этих регистров, что
|
|
Это почти работает. На самом деле это значит, что выражения 4.1 и 4.2 после каждого невидимого регистра были, по крайней мере однажды, обновлены. Пока этого не случилось, невидимые регистры в двух машинах могут иметь различные значения, потому что они могут быть инициализированы различными значениями.
Таким образом, мы должны сформулировать более слабую версию выражений 4.1 и 4.2. Мы используем тот факт, что невидимые регистры используются только для хранения промежуточного результата (именно поэтому они могут быть скрыты от программиста). Действительно, если невидимый регистр Rявляется входным регистром этапа k, тогда конвейерная машина использует этот регистр в цикле T только, если он был обновлен в конце предыдущего цикла. Более формально, мы имеем
|
Лемма 4.4 |
Пусть Iπ(k, T) = i и пусть R будет невидимым входным регистром этапа k, который не был модифицирован в конце цикла T — 1, тогда:
1. Набор выходных регистров R' этапа k, который обновлен в конце цикла T, не зависит от RT.
2. ПустьR' – выходной регистр этапа k который обновлен в конце цикла T и пусть S – входной сигнал для R', тогда ST не зависит от RT.
Это может быть проверено изучением таблиц 4.4 - 4.6 и 4.8.
Поэтому этого будет достаточно, чтобы доказать уравнения 4.2 для всех видимых регистров также как и для всех невидимых регистров, которые синхронизируются в конце цикла T. Этого также достаточно, чтобы доказать уравнение 4.1 для входных сигналов Sвсех регистров, которые синхронизируются в конце цикла T.
Согласно вышеупомянутым предположениям и гипотезам о зависимостях данных в выполняемых программах, мы теперь способны доказать, что машины DLXπи DLXσвыполняют одну и ту же последовательность обращений к памяти. Таким образом, CPU моделируют друг друга в том смысле, что они имеют одинаковое поведение ввода/вывода в память. Гипотезы о зависимостях данных будут удалены позже, когда мы представим логику пересылки и аппаратную взаимную блокировку.
|
Теорема 4.5 |
Предположим, что для всех i >= 0 и для всех r=/=0, команды Ii-3,..., Ii-1 не пишут в регистр GPR[r], где GPR[r] исходный операнд команды Ii. Тогда должны удовлетворяться следующие два требования для всех циклов T и T', для всех этапов k, и для всех команд Ii которые
|
|
1. Для всех сигналов S на этапе k, которые являются входами в регистр R€ out(k), который обновляется в конце цикла T:
|
|
2. Для всех регистров и R€ out(k), которые являются видимыми или обновляемыми в конце цикла T:
![]()
|
ДОКАЗАТЕЛЬСТВО |
Доказательство индукцией по циклам T конвейерного исполнения. Пусть T = 0. Мы имеем IП(0,0) = 0 = Ia(0,0), т.е., команда 0 на этапе 0 машины DLXπв течении цикла T = 0 и на этапе 0 машины DLXσв течении цикла T' = 0. Единственный вход этапа 0 – адрес для памяти команд. Этот адрес является входом регистра DPCдля машины DLXσи сигналом dpcдля машины DLXπ. Конструктивно, оба сигнала имеют в соответствующих циклах T = 0 и T' = 0 одно и то же значение, а именно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.