Проектирование системы профилактики АТС, обеспечивающей безопасность дорожного движения (на примере Октябрьского района города Красноярска), страница 14

Автотранспортные средства и большинство сложных технических систем являются восстанавливаемыми объектами. Известно, что с момента ввода в эксплуатацию АТС и до предельного состояния, техническое состояние последних многократно восстанавливается путем замены деталей, узлов и агрегатов. В результате последовательных замен неисправных, либо дефектных элементов, образуется так называемый накопленный процесс восстановления. Напомним, что технический ресурс – наработка элементов АТС до их предельного состояния.

Процесс восстановления – это последовательность восстановления работоспособности объекта за весь срок его службы путем проведения разборочно-сборочных, регулировочных, смазочных работ, либо замены нового элемента или отремонтированного.

Процесс восстановления оценивается количественными показателями: интегральной и дифференциальной функциями восстановления. В соответствии с ГОСТ 27. 00. 89 используются следующие характеристики: ведущая функция  и параметр потока отказов (замен) . В этих терминах словосочетание «поток отказов (замен)» отождествляется с восстановлением, так как восстановление работоспособности автотранспортных средств осуществляется как при профилактической замене или при текущем ремонте. По характеристикам процесса восстановления представляется возможным рассчитывать и планировать расход запасных частей, создавать новые способы расчета и управлять качеством материально-технического обеспечения на стадии проектирования, изготовления АТС и эксплуатации.

Процесс восстановления можно представить в виде математической модели как последовательность положительных, взаимно независимых случайных чисел, каждое из которых имеет свое распределение. Например, технический ресурс или наработка элементов автомобиля  между последовательными заменами и составляют процесс его восстановления. При этом каждое из чисел в общем случае может иметь свой закон распределения с функциями .

Важным понятием в теории восстановления является понятие композиции законов распределений. Композиция распределений

                                                  (28)

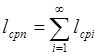                                                                (29)

Композиция имеет ряд общих свойств, не зависящих от вида законов распределений, и частных свойств, применимых к конкретным распределениям. Два общих свойства6

1) математическое ожидание композиции равно сумме математических ожиданий ее составляющих:

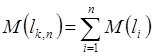                                           (30)

2) дисперсия композиции равна сумме дисперсии ее составляющих:

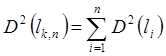                                         (31)

К частным свойствам композиции относятся следующие положения:

1) при композиции нескольких распределений Пуассона тоже получается распределение Пуассона;

2) композиция нескольких нормальных распределений дает нормальное распределение;

3) композиция большого количества распределений кроме закона Вейбулла – Гнеденко в итоге дает нормальное распределение.

6.1. Ведущая функция восстановления

Ведущая функция – одна из важнейших количественных характеристик, необходимая для: прогнозирования и планирования потребности запасных частей и материалов, трудовых ресурсов; оптимизации и управления качеством системы профилактики АТС в реальных условиях эксплуатации. Она используется, например, при определении оптимального момента профилактической замены элементов, при определении оборотного фонда агрегатов на планируемый период.

Функция восстановления рассчитывается как бесконечная сумма функций композиции распределения:

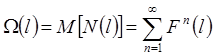                                 (32)

где  - n-кратная свертка функций распределений  отказами.