Проектирование системы профилактики АТС, обеспечивающей безопасность дорожного движения (на примере Октябрьского района города Красноярска), страница 10

,                                              (6)

.

2.2 Оценка параметра масштаба закона Вейбулла-Гнеденко

Точечная оценка параметра масштаба  закона Вейбулла-Гнеденко, рассчитывается по формуле,  тыс.км:

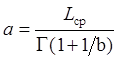,                                                 (7)

где  - гамма – функция по аргументу , который берется из табл.4 приложение 1 в зависимости от коэффициента вариации .

Значение гамма – функция определяем по табл.5 в зависимости от полученного значения коэффициента вариации. Чтобы найти, гамма – функцию воспользуемся тем же алгоритмом аналогично оценки параметра формы  закона Вейбулла-Гнеденко.

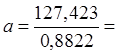144,437.                            

Получим соответственно нижнюю границу параметра масштаба

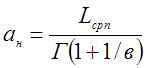                                                   (8)

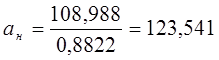
Верхнюю границу

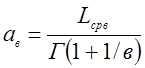                                                   (9)

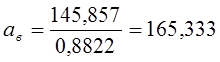
3 Проверка нулевой гипотезы

χ²_рас < χ²_табл(β,k) – условие соблюдение нулевой гипотезы.(10)

где     χ²_рас – значение критерия согласия Пирсона, вычисленное по экспериментальным данным; χ²_табл – критическая точка критерия ( по таблице № 6 [31] );

где     β – уровень значимости, k – число степеней свободы,

β = 0,1; где S – количество частных интервалов выборки,

r – Количество параметров предлагаемого распределения,

r = 2.

- определяем количество интервалов S по правилу Штюргеса с округлением до целого значение:

,                                             (11)

                                                                             где      – количество частичных интервалов выборки;

r – количество параметров предполагаемого распределения.

При двухпараметрическом законе Вейбулла-Гнеденко .

(табличное значение критерия )

- длину интервала как отношение размаха вариационного ряда на число интервалов, т.е. разность между наибольшим и наименьшим значениями вариационного ряда

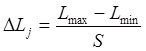,                                              (12)

.

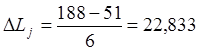- границы интервалов определяют по формуле

                                                                                                                

где j=1, 2, …, s.

Таблица 2 - Расчет эмпирических частот

- рассчитать, исходя из нулевой гипотезы теоретические частоты по формуле

,                                         (14)

где j = 1, 2, …, S.

или

,

- определить функцию распределения отказов, входящую в формулу (18), по формуле (для закона Вейбулла-Гнеденко):

,                                        (15)

где   – средняя наработка на замену (тыс.км),

 - точечная оценка параметра масштаба закона Вейбулла - Гнеденко в тыс. км.

Тогда

- рассчитаем :

Значит  равно:

Можно воспользоваться моделью оценивания функции распределения по нормальному закону распределения:

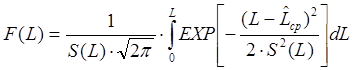                           (16)

или заменив переменную  - функция Лапласа. Получим:

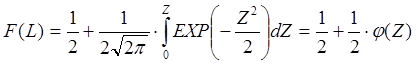                           (17)

Таблица 3 - Расчет - распределения согласия Пирсона

										/
1		0			73,83	5	25	0,1573	4,0898	6,11276
2		73,83			96,66	2	4	0,1361	3,5386	1,13039
3		96,66			119,49	4	16	0,1611	4,1886	3,81989
4		119,49			142,32	3	9	0,1622	4,2172	2,13411
5		142,32			165,15	4	16	0,1408	3,6608	4,37062
6		165,15			∞	8	64	0,2425	6,305	10,15067