Машиностроение \ Основы теории надёжности и диагностики

Проектирование системы профилактики АТС, обеспечивающей безопасность дорожного движения (на примере Октябрьского района города Красноярска), страница 13

Таблица 6  -  Основные значения вариационного ряда.  

X2расч

7,9498

N

21

Lср

46

D(L)

1266,3143

S(L)

35,5853

V

0,778429

b

12 924

Xe(2N)

28 144

Г

0,9247

a

49

Таблица  7 - Точечная оценка вероятности безотказной работы и интенсивности отказов.

L

Pв(L)

Pср(L)

Pн(L)

lymв(L)

lymср(L)

lymн(L)

0

1

1

1

0

0

0

10

0,9186

0,8809

0,7968

0,011

0,0164

0,0294

20

0,8122

0,7331

0,5733

0,0134

0,0201

0,0359

30

0,7037

0,5919

0,3909

0,0151

0,0226

0,0405

40

0,6007

0,4674

0,256

0,0165

0,0246

0,044

50

0,5066

0,3625

0,1624

0,0176

0,0262

0,047

60

0,4229

0,2768

0,1002

0,0185

0,0277

0,0496

70

0,3498

0,2086

0,0603

0,0194

0,0289

0,0518

80

0,287

0,1552

0,0355

0,0202

0,0301

0,0539

90

0,2338

0,1143

0,0205

0,0209

0,0311

0,0558

100

0,1891

0,0833

0,0116

0,0215

0,0321

0,0575

110

0,152

0,0601

0,0065

0,0221

0,033

0,0592

120

0,1215

0,043

0,0036

0,0227

0,0339

0,0607

130

0,0965

0,0305

0,0019

0,0232

0,0347

0,0621

140

0,0763

0,0215

0,001

0,0238

0,0354

0,0635

150

0,06

0,015

0,0005

0,0242

0,0362

0,0648

160

0,047

0,0104

0,0003

0,0247

0,0369

0,066

170

0,0366

0,0072

0,0001

0,0251

0,0375

0,0672

180

0,0284

0,0049

0,0001

0,0256

0,0381

0,0683

190

0,022

0,0034

0

0,026

0,0388

0,0694

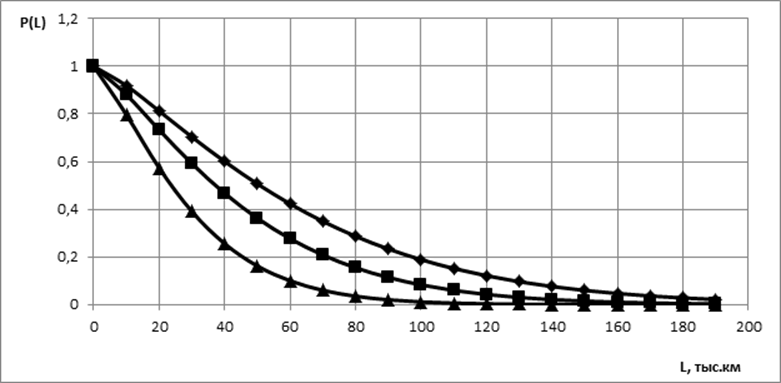
Рисунок 4 – График вероятности безотказной работы до второй замены системы (элемента).

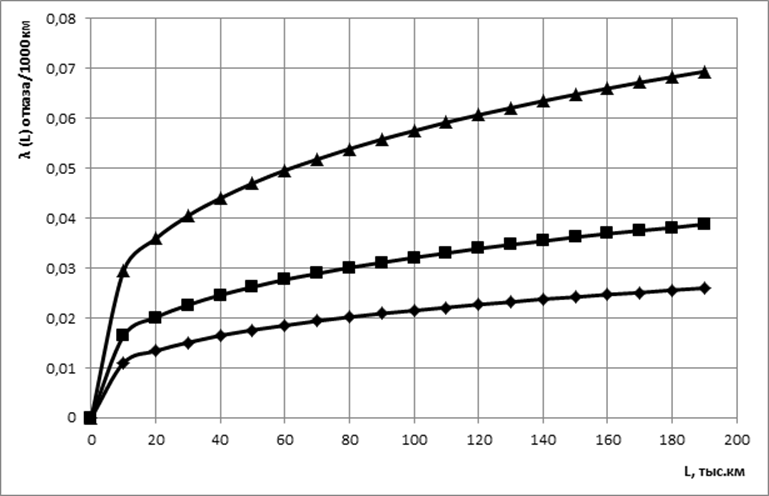
Рисунок 5 - График интенсивности отказов системы (элементов) до второй замены

Таблица 8 – Плотность распределения наработки до второй замены

L

f(L)

L

f(L)

0

0

100

0,00268

10

0,01443

110

0,00199

20

0,01471

120

0,00146

30

0,01337

130

0,00106

40

0,01149

140

0,00076

50

0,00951

150

0,00054

60

0,00766

160

0,00038

70

0,00604

170

0,00027

80

0,00467

180

0,00019

90

0,00356

190

0,00013

100

0,00268

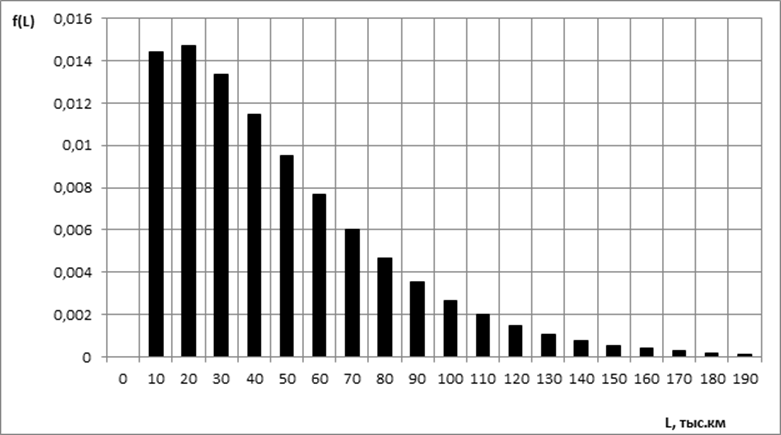
Рисунок 6 - График плотности распределения отказов до второй замены

 6 Оценка  показателей процесса восстановления (графоаналитический метод)

Теория восстановления возникла как наука при решении частных задач теории вероятности. Она изучает сложные виды закономерностей распределения случайных величин, образующихся при их суммировании, смешивании и наложении во времени.

Скачать файл