Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача: Методические указания к выполнению контрольных заданий, страница 8

Значение линейной формы F  при этом допустимом решении равно F₂=2, т.е. значение целевой функции увеличилось.

Примем за свободные переменные x₂ и x₄., т.е. те переменные, которые в этом решение равны 0. С этой целью из второго уравнения системы (1.21) выразим x₅  Получим. Тогда

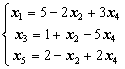 (1.22)

Для увеличения значения F будем увеличивать x₄. Проведя аналогичный анализ системы (1.22), заключаем, что, что x₄ можно увеличить до 1/5. (Следует из рассмотрения  второго уравнения системы (1.22)). Таким образом, получим третье допустимое решение x₁=28/5, x₂=0 , x₃=0, x₄ =1/5 , x₅=12/5 или (28/5,0,0, 1/5, 12/5). Значение линейной формы F  при этом допустимом решении равно F₃=11/5, т.е. значение целевой функции увеличилось.

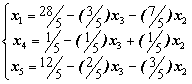 (1.23)

Так как в последней линейной форме обе свободные переменные входят с отрицательными коэффициентами, то наибольшее значение достигается при x₂=0 , x₃=0.

Из этого следует, что решение (28/5,0,0, 1/5, 12/5) является оптимальным и F_max=11/5.

Для того, чтобы упростить трудоемкие операции по пересчету коэффициентов и  перезаписи системы ограничений, можно выполнять преобразования специальной симплекс-таблицы.

Симплексные таблицы

Для составления этой таблицы систему фазовых ограничений и целевую функцию необходимо записать в стандартной форме, т.е. сведенной к единичному базису:

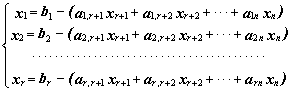 (1.24)

  (1.25)

В виде таблицы эти данные можно представить так:

Таблица 1.1