Отчет по устойчивости
Отчет по устойчивости (рис.2.7) состоит из двух таблиц. В таблице 1 приводятся:
· результат решения задачи;
· нормированная стоимость, которая показывает, насколько изменится (уменьшится) целевая функция при принудительном включении единицы этой продукции в оптимальное решение; значение отлично от 0, когда соответствующий вид продукции не входит в оптимальный план и наоборот;
· коэффициенты целевой функции;
· предельные значения приращения коэффициентов целевой функции, при которых сохраняется структура оптимального решения.
В нашем примере можно сказать, что при принудительном строительстве одного квадратного метра жилья в кирпичном доме целевая функция уменьшится на 4 единицы, при принудительном строительстве одного квадратного метра панельного жилья - на 2 единицы. Структура оптимального решения не меняется при изменении величины прибыли в следующих диапазонах:
· для блочного жилья – [5-0.25;5+1]=[4,75;6];
· для панельного жилья – [7-1E+30;7+2], но так как величина прибыли ограничена снизу нулем, получаем диапазон [0;9];
· для жилья в кирпичном доме – [0;10];
· для жилья в монолитном доме – [8.5;10].
В таблице 2 приводятся аналогичные значения для ограничений:
· величина использованных ресурсов;
· теневая цена, которая показывает, как изменится целевая функция при изменении ресурсов на единицу. Для ресурсов, использованных не полностью, теневая цена равна 0 и наоборот;
· значения приращения ресурсов, при которых сохраняется структура оптимального решения.

Рис.2.7 Отчет по устойчивости
Можно, например, сказать, что если бы у нас была возможность увеличить количество трудовых ресурсов на единицу, целевая функция увеличилась бы на 4,5 единиц. А структура оптимального решения не изменится при изменении фактического наличия трудовых ресурсов в диапазоне [60-2;60+20]=[58;80].
Отчет по пределам
Этот отчет приведен на рис.2.8. В нем показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.
 Рис.2.8 Отчет по пределам
Рис.2.8 Отчет по пределам
Приводятся значения xj в оптимальном решении, нижние и верхние пределы изменения значений xj и значения целевой функции на этих пределах.
Решение с введением дополнительных переменных – неиспользованных ресурсов.
Введем дополнительные переменные:
y1 – остатки электроэнергии,
y2 – остатки трудовых ресурсов,
y3 – остатки картофеля,
y4 – остатки муки,
y5 – остатки масла.
Тогда математическая модель нашей задачи примет следующий вид:
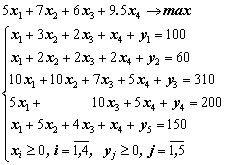
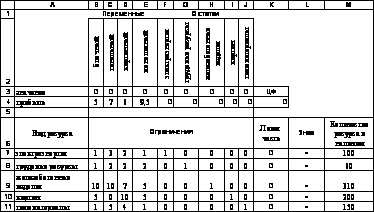 |
Рис.2.9 Исходные данные задачи с дополнительными переменными
В ячейку К4 введена формула =СУММПРОИЗВ(B3:J3;B4:J4), в ячейку К7 введена формула =СУММПРОИЗВ($B$3:$J$3;B7:J7), затем она скопирована в ячейки К8:К11.
Диалоговое окно Поиска Решения показано на рис.2.9. Результаты решения – на рис.2.10.
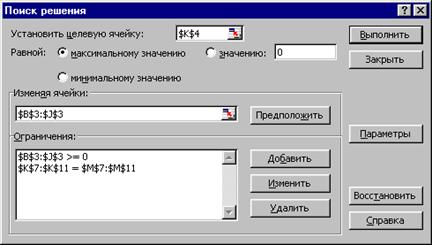
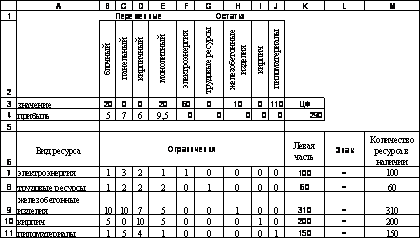 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.