Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача: Методические указания к выполнению контрольных заданий, страница 12

Рис.1.9. Симплекс таблица после второй итерации.

В строке, соответствующей целевой функции, нет отрицательных элементов, следовательно, получено оптимальное решение (28/5,0,0, 1/5, 12/5) и F_max=11/5. Заметим, что решения совпали.

2. ЗАДАЧА ОБ ОПТИМАЛЬНОМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования, которая записывается следующим образом:

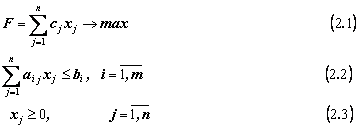
Здесь (2.1) - целевая функция; (2.2) - система ограничений; (2.3) - естественные граничные условия;

x_j– количество выпускаемой продукции j-го типа, j=1,2, …n;

b_i - количество располагаемого ресурса i-го вида, i=12,….,m;

a_ij- норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

c_j- прибыль, получаемая от реализации единицы продукции j-го типа.

В этом случае значение целевой функции - это суммарная величина прибыли от реализации продукции, выпущенной в объемах x₁,x₂,...x_n. Левая часть неравенства (2.2) представляет собой общее количество ресурса i, используемое в соответствии с планом, правая часть -  это имеющийся запас.

            Эта задача является частным случаем общей задачи линейного программирования, теория применения которого была изучена в курсе Высшей математики [5]. Основными положениями этой теории являются следующие положения:

Каждой задаче линейного программирования соответствует двойственная задача, которая записывается по следующим правилам:

1.  Каждому i-му ограничению исходной задачи соответствует переменная двойственной задачи z_i(двойственная переменная)

2.  Каждой j-ой переменной исходной задачи соответствует ограничение двойственной. Матрица коэффициентов ограничений двойственной задачи является транспонированной матрицей ограничений исходной. Если в исходной задаче ограничения имеют знак £, то в двойственной - ³

3.  Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи

4.  Если исходная задача была на нахождение максимума, то двойственная будет на нахождение минимума:

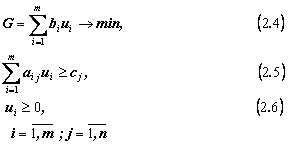
§  Для оптимального решения значения целевых функций прямой и двойственной задач совпадают (maxF=minG).

§  Если это записать в форме , то видно, что двойственная переменная u_iявляется коэффициентом при b_i и, следовательно, показывает, как изменится целевая функция при изменении ресурса b_i на единицу. В литературе по оптимизации двойственные переменные принято называть двойственными оценками. В отчетах Excel двойственная оценка называется теневой ценой.

§  Теневая цена ресурса отлична от нуля (точнее больше нуля) только для тех видов ресурсов, которые используются полностью, т.е. ограничения (2.2) превращаются в равенства.

Принцип дополняющей полужесткости !!!!!!

§  Симметричность прямой и двойственной задач заключается в том, что значения теневой цены в прямой задаче совпадают с решением двойственной и наоборот

§  В теории ЛП также рассматриваются дополнительные двойственные переменные, которые в Excel называются нормированной стоимостью. Каждой основной переменной x_j соответствует своя нормированная стоимость v_j. Известно, что если x_j=0 (т.е. продукцию j-го типа выпускать не целесообразно), то v_j отлична от нуля (точнее v_j<0) и наоборот, если x_j>0 (продукцию выпускать целесообразно), то соответствующее v_j=0. Экономический смысл нормированной стоимости - это величина, которая показывает, на сколько уменьшится значение суммарной прибыли (ЦФ), при принудительном выпуске этой продукции.