Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача: Методические указания к выполнению контрольных заданий, страница 6

Вывод. Целевая функция не ограничена, если многогранник незамкнут в направлении роста целевой функции

ПРИМЕР 5

Решить графически задачу ЛП (1.16)-(1.18).

 (1.16)

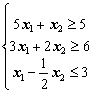                   (1.17)

                          (1.18)

Решение.

Построим область допустимых решений D (Рис.1.4), она совпадает с областью в примере 3.

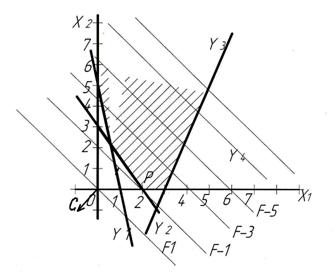
Рис. 1.4

Заметим, что вектор-градиент  направлен в противоположную сторону (по сравнению с рис.1.3). Максимум достигается в единственной точке Р, являющейся точкой пересечения оси x₁   и y₂.

Координаты точки Р можно определить, решив систему уравнений:

Ее решение x₁=2,  x₂=0, значение функции в этой точке равно

Вывод. Задача ЛП имеет единственное решение, когда многогранник замкнут в направлении роста целевой функции.

Рассмотренные примеры  иллюстрируют все возможные варианты Положения 5.

ОСНОВНАЯ ИДЕЯ СИМПЛЕКС-МЕТОДА

Если ранг матрицы А системы (1.1) и ранг расширенной матрицы системы равен r(r£m), то rпеременных  могут быть выражены через остальные  переменные:

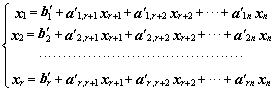 (1.19)

Переменные (неизвестные) называются базисными, а весь набор () – базисом, остальные переменные называются свободными. Система ограничений (1.19) называется системой приведенной к единичному базису. Подставляя  в линейную форму F (1.3) вместо базисных переменных их выражения через свободные переменные из системы (1. 19) получим:

 (1.20)

Полагая все свободные переменные равными нулю, найдем значения базисных переменных: . Если все значения , решение () системы ограничений является допустимым. Такое допустимое решение называется базисным или опорным, обозначим его через . Для полученного базисного решения значение целевой функции . Решение задачи при помощи симплекс-метода состоит из ряда шагов, состоящих в том, что от данного базиса  переходим к другому базису  с таким расчетом, чтобы значение целевой функции F увеличивалось, или, по крайней мере не уменьшалось, т.е. .

Геометрическая интерпретация симплекс-метода состоит в том, что аналитическому переходу от одного базиса к другому соответствует переход от одной вершины многоугольника множества допустимых решений к другой, в которой целевая функция имеет не меньшее значение. Этот факт основан на том, что вершинам многоугольника множества допустимых решений соответствуют опорные решения системы ограничений.