Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача: Методические указания к выполнению контрольных заданий, страница 5

                         (1.12)

Решение.

Заметим, что система фазовых ограничений (1.11) совпадает с системой (1.9). Поэтому область допустимых решений D. будет той же самой, что и в примере 2.

Построим вектор-градиент  из начала координат. Проведем линию перпендикулярно вектору . Линия F1, проходящая через начало координат, соответствует значению 1, поскольку . Мысленно сдвинем линию уровня в направлении вектора . Первое касание многоугольника соответствует положению F3 . Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Продолжим движение линии уровня до выхода из множества D,. этому положению соответствует  положение F8 . Заметим, что линия уровня параллельна стороне MN , поэтому решением является множество точек лежащих между крайними точками M и N, Точка M является точкой пересечения прямых y₃ и y₄, ее координаты можно определить как решение линейной системы.

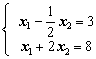
Ее решение x₁=4,  x₂=2, и этой точке соответствует искомое максимальное значение линейной функции

 .

 Таким образом,  F_max=9, при   x₁=4,  x₂=2

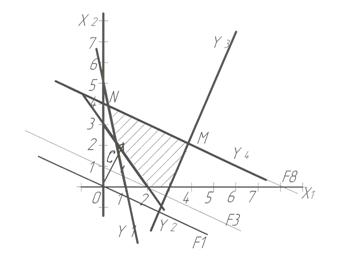
Рис.1.2

Точка N является точкой пересечения прямых y₁ и y₄, ее координаты можно определить как решение линейной системы

Ее решение x₁=2/9, x₂=35/9, и этой точке соответствует искомое максимальное значение линейной функции . Таким образом, значение в точке N совпадает со значением в точке M. F_max=9, при x₁=2/9,  x₂=35/9.

Координаты всех точек, лежащих между M и N можно записать в виде

Значение функции во всех этих точках  равно 9.

Вывод. В данном случае линейная функция достигает своего максимального значения во всех точках ребра MN множества решений D.

ПРИМЕР 4

Решить графически задачу ЛП (1.13)-(1.15).

 (1.13)

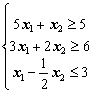               (1.14)

                       (1.15)

Решение.

Построим область допустимых решений D (Рис.1.3).

Построение области аналогично примеру 2, но в этом построении отсутствует прямая y₄.

Пересечение трех полуплоскостей определяют неограниченную область допустимых решений D.

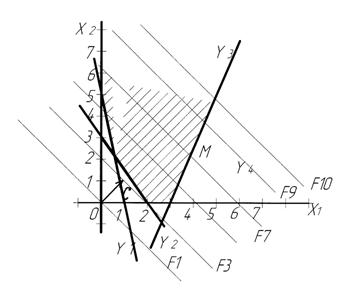
Рис. 1.3

Построим вектор-градиент  из начала координат. Проведем линию перпендикулярно вектору-. Линия F1, проходящая через начало координат, соответствует значению 1, поскольку  . Мысленно сдвинем линию уровня в направлении вектора . Первое касание многоугольника соответствует положению F3 . Эта линия является опорной, и ей соответствует минимальное значение , которое достигается на множестве допустимых решений. Заметим, что многогранник незамкнут в направлении роста целевой функции, поэтому целевая функция не имеет максимума, поскольку для любой линии уровня найдется другая линия уровня, лежащая в направлении вектора , которой соответствует большее значение функции.