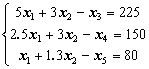Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача: Методические указания к выполнению контрольных заданий, страница 3

        (1.8)

        (1.9)

Соотношения (1.7) - (1.9) определяют задачу ЛП в канонической форме.

СИМПЛЕКС-МЕТОД

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ

Геометрическое истолкование симплекс-метода наиболее просто может быть проиллюстрировано в случае двух переменных.

Положение 1.

Каждое неравенство с двумя переменными x₁ и  x₂ определяет полуплоскость в системе координат    x₁ 0 x₂.

Положение 2.

В случае, когда задана система неравенств

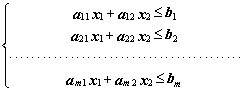 (1.4), то она определяет многоугольную область D на плоскости, которая является результатом пересечения m полуплоскостей. Область D называется областью решений системы неравенств. Область D может быть ограниченной, неограниченной или пустой. Область решений D обладает важным свойством – она является выпуклой.

Определение 1. Область называется выпуклой, если она  вместе с любыми двумя точками содержит весь отрезок их соединяющий.

Определение 2. Прямая называется опорной по отношению к области, если:

1.  имеет с областью по крайней мере одну общую точку;

2.  вся область лежит по одну сторону от этой прямой.

Положение 3. Пусть задана линейная функция

 .  (1.5)

Для каждой точки плоскости в системе координат  x₁ 0 x₂. функция F  принимает фиксированное значение F=F₁.

Определение 3. Множество точек, в которых функция принимает фиксированное значение, называется линией уровня.

Линия уровня для линейной функции – прямая, которая определяется уравнением . Придавая F₁ различные значения, получим различные линии уровня.

Все линии уровня (для линейной функции)  параллельны между собой.

Нормаль к линии уровня определяется через градиент функции. Градиент произвольной функции двух переменных f(x_1,x₂) может быть вычислен по формуле

  (1.6), поэтому градиент линейной функции определяется уравнением , т.е. градиент может быть задан вектором , выходящим из начала координат.

Градиент указывает направление наибыстрейшего роста функции в данной точке.

Положение 4. Графическое решение задачи ЛП, определяемой фазовыми ограничениями (1.4) и целевой функцией (1.5), основано на мысленном эксперименте по перемещению линии уровня относительно области допустимых решений D. Пусть при движении прямой F₁ в положительном направлении вектора   она впервые встретится с многоугольником решений в его вершине, тогда в этом положении прямая F₁ становится опорной, и на этой прямой функция F принимает наименьшее значение. При дальнейшем движении в том же направлении  прямая F₁ пройдет через другую вершину многоугольника решений (выходя из области решений), и станет также опорной прямой; на ней функция F принимает наибольшее значение  среди  всех значений, принимаемых на многоугольнике решений.

Таким образом, максимизация линейной функции  на многоугольнике решений достигается в точке пересечения этого многоугольника с опорными прямыми, перпендикулярными вектору .