Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача: Методические указания к выполнению контрольных заданий, страница 7

Решение симплекс-методом заканчивается, когда среди опорных решений будет найдено такое, которое обеспечивает максимум линейной формы (1.3). Такое решение называется оптимальным.

РЕАЛИЗАЦИЯ СИМПЛЕКС-МЕТОДА

Рассмотрим идею симплекс-метода на конкретном примере

  (1.21)

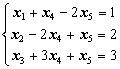     (1.22)

                (1.23)

Решение. Данная система уравнений ограничений совместна, так как ранги матрицы системы

и расширенной системы

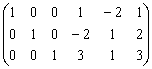
совпадают и равны 3. Следовательно, три переменные (базисные) можно линейно выразить через две свободные переменные. Выразим, например, x₁, x₂ и x₃ через x₄ и x₅, т.е. приведем систему к единичному базису:

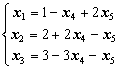                                                (1.21)

Линейная форма  уже выражена через x₄ и x₅.

При x₄ =0 и x₅=0, найдем значение базисных переменных x₁=1, x₂=2 и x₃=3.

Таким образом, первое допустимое решение имеет вид x₁=1, x₂=2 , x₃=3, x₄ =0 , x₅=0 или (1,2,3,0,0). При найденном допустимом решении линейная форма F имеет значение 0, т.е. F₁=0.

Теперь попытаемся увеличить значение F:

-  увеличение x₄уменьшит F , так как перед x₄стоит отрицательный коэффициент, а

увеличение x₅ даст увеличение и F₁;

-  будем  увеличивать x₅  таким образом, чтобы одна из базисных переменных (x₁ или x₂или x₃) обратилась в ноль, а остальные базисные переменные оставались бы неотрицательными.

Анализируя первое уравнение системы (1.21) приходим к выводу, что x₅ можно увеличить неограниченно. При этом x₁ остается положительным и никогда не обратиться в ноль. Из второго уравнения системы (1.21) следует, что x₅ можно увеличить до 2 (больше увеличивать нельзя, т.к. x₂ станет отрицательным). Из третьего уравнения системы (1.21) следует, что x₅ можно увеличить до 3. Принимая во внимание приведенный анализ, приходим к выводу, что x₅=2.

Таким образом, получим второе допустимое решение x₁=5, x₂=0 , x₃=1, x₄ =0 , x₅=5 или (5,0,1,0,2).