Положение 5. Существование решения и количество решений задачи ЛП основано на анализе взаимного положения области допустимых решений D и линии уровня.
Если область D ограничена, то возможны два варианта:
А) опорная прямая имеет с многоугольником одну общую точку – одно решение.
Б) опорная прямая параллельна стороне многоугольника – множество решений ( вся сторона многоугольника).
Если область D не ограничена, то возможны также два варианта:
А) опорная прямая имеет с многоугольником одну общую точку – одно решение;
Б) не существует опорной прямой (в направлении роста функции) - множество решений пусто (нет решений).
ПРИМЕР 2
Решить графически задачу ЛП (1.7)-(1.9).
![]() (1.7)
(1.7)
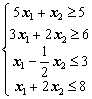 (1.8)
(1.8)
![]() (1.9)
(1.9)
Решение.
Построим область допустимых решений.
Первое неравенство системы (1.8) задает полуплоскость,
границей которой является прямая y1, определяемая
равенством ![]() . Построим эту прямую на координатной
плоскости x1 0 x2
(рис.1.1), искомой полуплоскостью (она заштрихована) будет, та, которая лежит
выше этой прямой.
. Построим эту прямую на координатной
плоскости x1 0 x2
(рис.1.1), искомой полуплоскостью (она заштрихована) будет, та, которая лежит
выше этой прямой.
Второе неравенство задает полуплоскость, границей
которой является прямая y2, определяемая равенством ![]() . Также построим прямую y2
на координатной плоскости и заштрихуем соответствующую полуплоскость.
. Также построим прямую y2
на координатной плоскости и заштрихуем соответствующую полуплоскость.
Аналогично построим полуплоскости, соответствующие
неравенствам три и четыре, их границы y3 и y4,
определяются уравнениями ![]() и
и ![]() соответственно.
соответственно.
Пересечение этих четырех плоскостей определяют область допустимых решений D.
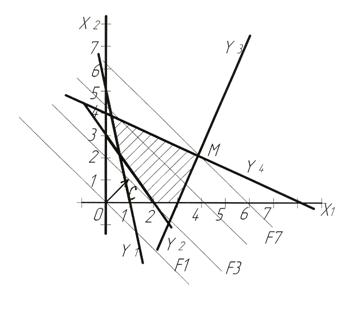
Рис. 1.1
Построим вектор-градиент ![]() из
начала координат. Проведем линию перпендикулярно вектору-
из
начала координат. Проведем линию перпендикулярно вектору-![]() . Линия F1, проходящая
через начало координат, соответствует значению 1, поскольку
. Линия F1, проходящая
через начало координат, соответствует значению 1, поскольку ![]() . Мысленно сдвинем линию уровня в
направлении вектора-
. Мысленно сдвинем линию уровня в
направлении вектора-![]() . Первое касание
многоугольника соответствует положению F3 . Эта линия является
опорной, и ей соответствует минимальное значение , которое достигается на
множестве допустимых решений. Продолжим движение линии уровня до выхода из
множества D,. этому положению соответствует положение F7
. Рассмотрим крайнюю точку M , которая является точкой
пересечения прямых y3 и y4,
ее координаты можно определить как решение линейной системы.
. Первое касание
многоугольника соответствует положению F3 . Эта линия является
опорной, и ей соответствует минимальное значение , которое достигается на
множестве допустимых решений. Продолжим движение линии уровня до выхода из
множества D,. этому положению соответствует положение F7
. Рассмотрим крайнюю точку M , которая является точкой
пересечения прямых y3 и y4,
ее координаты можно определить как решение линейной системы.
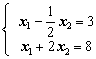
Ее решение x1=4 x2=2,
и этой точке соответствует искомое максимальное значение линейной функции ![]() . Таким образом, Fmax=7
при x1=4 x2=2.
. Таким образом, Fmax=7
при x1=4 x2=2.
Вывод. В данном случае линейная функция достигает своего максимального значения в крайней точке множества решений.
ПРИМЕР 3
Решить графически задачу ЛП (1.10)-(1.11).
![]() (1.10)
(1.10)
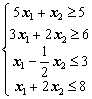 (1.11)
(1.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.