Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача: Методические указания к выполнению контрольных заданий, страница 2

Соотношения (1.1) принято называть фазовыми ограничениями, соотношения (1.2) – естественными ограничениями

Функцию F принято называть целевой функцией.

Система ограничений всегда может быть приведена к каноническому виду

Если ограничения заданы неравенствами, то их можно преобразовать в равенства путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих) ресурсов.

Так, например, в неравенстве   достаточно добавить к левой части некоторую величину xn+1³0  и получится равенство

Чтобы балансовые переменные не влияли на искомый оптимум, их вводят в целевую функцию (1.1) с нулевыми коэффициентами.

В дальнейшем будет рассматриваться только задача на максимизацию. Если необходимо решить задачу на минимизацию линейной формы, то коэффициенты целевой функции следует умножить на (-1) и решать эту новую задачу на максимум. Искомый минимум целевой функции получается умножением найденного максимального значения на (-1), т.е. .

Задачу ЛП, определяемую соотношениями (1.1)-(1.3), можно записать в матричном виде:

AX=B

X>0

CX®max

где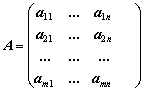               

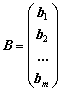
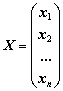
В дальнейшем при анализе задачи также используется расширенная матрица системы (1.1) , которая составляется из матрицы А и вектора В.

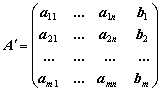
ПРИМЕР 1

Составить задачу ЛП, позволяющую оптимизировать расход кормов, и привести ее к каноническому виду.

Для откорма животных употребляют два вида кормов; стоимость 1 кг кормов I вида - 5у.е., а корма II вида - 2 у.е. В каждом килограмме корма I вида содержится 5 ед. питательного вещества А, 2.5 ед. питательного вещества B и 1 ед. питательного вещества C. В каждом килограмме корма II вида содержится соответственно 3, 3 и 1.3 ед. Суточный рацион предусматривает питательных единиц A не менее 225 ед., типа B  - не менее 150 ед. и типа C – не менее 80 ед. Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты были минимальны?

Решение

Обозначим через x₁ и x₂ количество кормов I и II вида соответственно. Тогда суммарная стоимость кормов будет равна 5 x₁ +2 x₂. Поэтому целевая функция будет иметь вид:

 (1.4)

Ограничения по содержанию питательных веществ в рационе будут иметь вид:

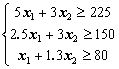               (1.5)

                      (1.6)

Соотношения (1.4)-(1.6) корректно определяют задачу ЛП, но предложенная форма записи не является канонической. Для приведения задачи к этой форме домножим ЦФ (1.4) на –1, в результате получим новую ЦФ (1.7). Для преобразования фазовых ограничений (1.5) к канонической форме введем положительные балансовые переменные x₃, x₄ и x₅. Тогда фазовые ограничения примут вид (1.8), а фазовые вид (1.9).

          (1.7)