Общая характеристика висячих и вантовых мостов. Элементы висячих и вантовых мостовых конструкция и материалы, страница 13

у – стрела провисания кабеля в рассматриваемом сечении.

(для формулы, приведенной выше, особенно актуален т.н. закон больших чисел: 102 – 101 = 1, а 102 – 100 = 2 – разница вторых слагаемых 1%, а разница результатов 50%).

8.3. Трехпролетные висячие мосты

Трехпролетные висячие мосты различают:

– по соотношению длин пролетов (и способу их закрепления);

– по типу балок жесткости (разрезные, неразрезные).

Трехпролетные мосты с разрезными балками жесткости

а) Мосты с подвешиванием к кабелю боковых пролетов, устраивают при соотношении       0,25×L₂ < L₁ £ 0,5´L_{2 .}       Принципиальная схема такого моста показана на рис. 8.11.

Рис. 8.11. Схема моста с подвешенными боковыми пролетами

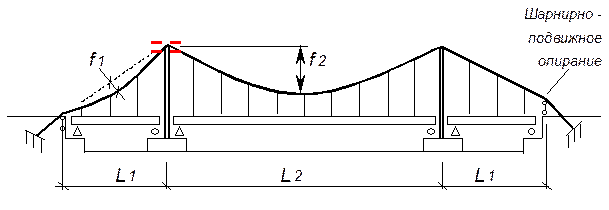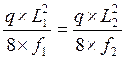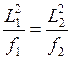Для обеспечения равенства   Н₁=Н₂,      т.е.      имеем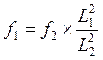  

здесь:       f1,   f2 – стрелки провисания кабеля в крайних и среднем пролетах.

б) Мосты с не подвешиванием к кабелю боковых пролетов устраивают при соотношении       L₁ £ 0,25´L_{2 .}       Принципиальная схема и фотография такого моста показаны на рис. 8.12 и 7.30. С точки зрения статической работы висячая часть системы аналогична однопролетной висячей схеме.

Рис. 8.12. Схема моста с не подвешенными боковыми пролетами

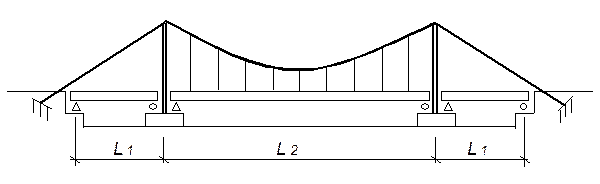Трехпролетные мосты с неразрезными балками жесткости

а) Мосты с подвешиванием к кабелю боковых пролетов, устраивают при соотношении       0,25×L₂ < L₁ £ 0,5´L_{2 .}       Принципиальная схема и фотография такого моста показана на рис. 8.13 и 8.14.

Рис. 8.13. Схема моста с подвешенными боковыми пролетами

Рис. 8.14. Трехпролетный висячий мост (Швеция)

б) Мосты с не подвешиванием к кабелю боковых пролетов устраивают при соотношении       L₁ £ 0,25´L_{2 .}       Принципиальная схема и фотографии таких мостов показаны на рис. 8.15 и 8.16.

Рис. 8.15. Схема моста с не подвешенными боковыми пролетами

 

Рис. 8.16. Трехпролетные висячие мосты (Финляндия)

Сравнивая предложенные выше схемы по соотношению пролетов и способу их закрепления, можно сделать несколько выводов:

1. По соотношению пролетов лучше, если     L₁ £ 0,25´L₂ ,     т.к. при этом кабель в боковых пролетах прямолинеен, деформации его упругие, следовательно – жесткость системы выше;

2. Боковые пролеты, обычно не подвешивают (если имеется такая возможность), т.к. при этом конструкция упрощается;

3. Боковые пролеты могут иметь разную длину(хотя обычно по длине они одинаковы).

Сравнивая предложенные выше схемы по типу балки жесткости (разрезные, неразрезные), можно сделать несколько выводов:

1. Неразрезность балок позволяет несколько уменьшить ширину промежуточных опор (т.к. на опоре установлена одна опорная часть);

2. Неразрезность балок позволяет уменьшить число деформационных швов на пролетном строении (их может быть всего два);

3. Однако кроме этого неразрезность балок практически ничего не дает, а иногда может ухудшить показатели системы т.к.:

а) Неразрезные балки несколько жестче, поэтому будут брать на себя бóльшую долю временной нагрузки с кабеля, снижая при этом экономичность системы;

б) При больших пролетах относительная жесткость балки уменьшается, поэтому неразрезность не приносит существенного уменьшения прогибов (по сравнению с разрезной системой), но в то же время увеличиваются температурные и силовые деформации;

в) Неразрезность приносит наибольший (ощутимый) экономический эффект лишь от действия постоянной нагрузки (см. рис. 8.17),

Рис. 8.17. Схемы к расчету балок

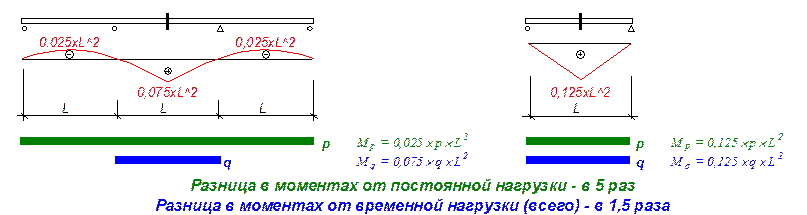а балки жесткости от действия постоянных нагрузок разгружены (см. п.8).

8.4. Многопролетные висячие мосты

Рис. 8.18. «Сан-Франциско – Окленд – Бей – Бридж» (Оклендский мост), США, 1930 г.

Системы многопролетных висячих мостов могут применяться при пересечении широких водных преград (где необходима большая длина сооружения) или в случае пересечения больших пространств при слабых грунтах (здесь необходимо большое количество сложных опор) однако в практике мостостроения, такие системы применяются крайне редко.