Представленная ниже математическая модель описывает взаимодействие полидисперсных У. частиц не только непосредственно в зоне теплового источника - дуги, но и рассматривает процессы дальнейшего реагирования активированного плазмой потока аэросмеси со свежей А., не прошедшей через эту зону или с “холодной” пароугольной смесью, подаваемой ниже электродуговой зоны, что характерно для комбинированных алло-автотермических методов газификации У.
Модель процесса характеризует двухфазный (полидисперсные У. частицы + газ-окислитель) химически реагирующий поток, распространяющийся в канале с внутренним источником тепла (электрическая дуга, плазменная струя или протекающие химические реакции) или без него.
Частицы и газ поступают в канал реактора с равной или разной температурами, между частицами, газом и тепловым источником имеет место тепломассообмен, а также учитывается радиационный обмен, обмен теплом и импульсом между потоком и стенкой канала. Кроме того, учитываются превращения топлива: выделение летучих продуктов из У. частиц, превращение летучих в газовой фазе и реакции газификации КО, а также образование оксидов серы и азота.
При разработке модели приняты следующие допущения: квазиодномерность и стационарность процесса; изотермичность частиц У.; скорости газового потока и частиц У. могут различаться между собой; для газов справедлив закон идеального состояния; смесь газа и частиц на входе в реактор однородна; взаимодействие частиц между собой и влияние множества частиц на силу сопротивления потоку пренебрежимо мало; зола является инертным компонентом.
Полидисперсность У. частиц отражается включением в эти уравнения определенного числа представительных фракций пылеугольного потока, выбираемых из гранулометрического распределения У. частиц по размерам, получаемого путем ситового анализа проб энергетических У. после мельницы.
С учетом принятых допущений система обыкновенных дифференциальных уравнений имеет следующий вид:
Уравнение концентрации газообразных компонентов
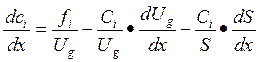, i=1,...,n. (19)
Уравнение концентраций твердых компонентов
|
|
, i = n + 1,...,N, l=1,...,L (20)
Уравнение движения частиц
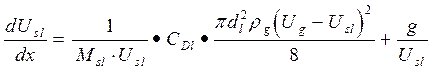, l=1,...,L. (21)
Уравнение температуры частиц
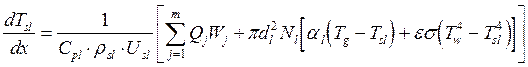, l=1,...,L. (22)
Уравнение сохранения импульса
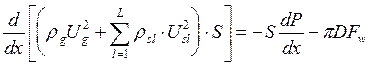(23)
Уравнение сохранения энергии
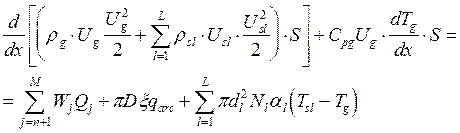(24)
Уравнение состояния идеального газа
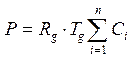(25)
Уравнения для времени пребывания газовой фазы и У. фракций в канале реактора
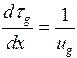, (26) 
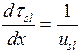. (27)
Тепловой вклад от дуги определяется в модели как разность между электрической мощностью и тепловыми потерями в стенку ПР:
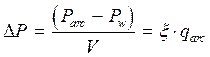, где 
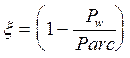- тепловой КПД
ПР; V - его объем.
Мощность электрической дуги выражается через мощность теплового потока в стенку:
,
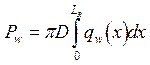который находится из эксперимента (LR - длина ПР).
При формировании начальных условий к системе уравнений (19-27) необходимо задать значения начальных скоростей и температур газа и частиц соответственно, давления на входе в реактор, температуру стенки при х = 0, массовые расходы газа и твердой фазы.
В уравнениях (19-27) обозначены:
Сi - объемные концентрации компонентов (кмоль×м-3); СD - коэффициент лобового сопротивления частиц; Ср - теплоемкость компонентов (Дж×кмоль-1×К-1); D - диаметр ПР (м); d - диаметр частиц (м); fi - источниковые члены, обусловленные изменением концентрации i-го компонента за счет химических реакций в единице объема в единицу времени (кмоль×м-3×с-1); М - масса частицы (кг); N - объемная концентрация частиц (м-3); DР - удельный тепловой вклад от дуги (Вт×м-3); Рarc - электрическая мощность дуги (Вт); Pw - тепловые потери в стенку (Вт); Qj - тепловой эффект j-й реакции (Дж×кмоль-1); F - сила сопротивления потоку (н); Р - давление (н×м-2); qarc - удельный тепловой поток от дуги (Вт×м-3); qw - удельный тепловой поток в стенку (Вт×м-3); Rg - 8,31×103 - универсальная газовая постоянная (Дж×кмоль×К-1); S - площадь поперечного сечения (м2); Т - температура (К).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
