виробництво
Статистичний контроль якості - контроль на всіх етапах виробництва, що у найвищому ступені відповідає економічному виробництву товарів, потрібних покупцю.
Статистичні показники якості продукції.
Як при виготовленні, так і при вимірюванні виникають дві категорії похибок: систематичні і випадкові.
Систематичні залежать від закономірних невипадкових чинників:
- неточного настроювання устаткування;
- похибки вимірювального інструмента;
- відхилення робочої температури.
Випадкові залежать від випадково діючих причин:
-припуску на обробку;
-механічних властивостей матеріалу.
В інженерній практиці часто виникає необхідність у визначенні:
- поля розсіювання параметрів;
- середнього значення;
- можливості отримання браку і т.п.
Усі ці
параметри часто є випадковими величинами, тому для їхнього аналізу використовують
теорію ймовірності.
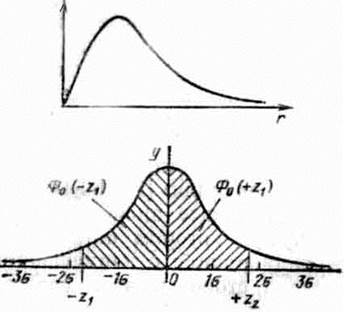
Залежність між числовими значеннями випадкової величини й імовірністю появи встановлює закон розподілу ймовірностей випадкової величини. Розсіювання ексцентриситетів, неспіввісності, радіального і торцевого биттів може відповідати закону Максвелла. Розсіювання відмови машин підпорядковане закону Вейбулла.
Лекція 03
Розподіл Гауса
Якщо
розсіювання значень випадкової величини залежить від великої кількості
факторів, і жоден із них не має переважного значення, тоді підпорядковується закону
нормального розподілу- закону Гаусса і записується рівнянням:
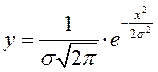
де у - щільність розподілу ймовірності;
е - основа натурального логарифма;
х - математичне очікування;
s - середнє квадратичне відхилення випадкової величини, яка визначає розсіювання значень випадкової величини відносно центру групування.
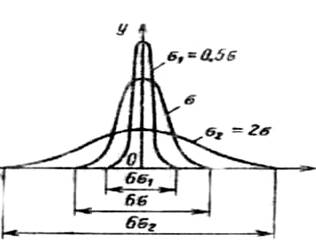
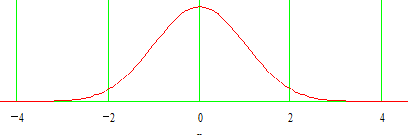
При розгляді властивостей і характеристик розподілу випадкових величин ми обмежимося нормальним, оскільки він найчастіше зустрічається.
Властивості характеристики розглянемо, користуючись графіком:
- найбільша щільність імовірності (Ymax) відповідає похибці х=0;
- при зростанні похибки ординати кривої симетрично зменшуються, іншими словами, чим більша похибка, тим менша щільність імовірності.
Розглянутий розподіл - теоретичний, тобто для ідеального випадку.
Визначення ймовірності процента деталей,
розмір яких лежить у заданому інтервалі
Площа, обмежена кривою, дорівнює ймовірності того, що випадкова величина лежить в інтервалі - ¥... + ¥.
Ця ймовірність визначається залежністю:
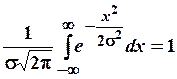
Змінюючи межі інтегрування,
можна визначити імовірність
попадання величини у заданий інтервал.
Виразивши випадкову величину Х в частках s, тобто прийнявши Х/s=Z і обчисливши, була складена таблиця інтеграла Лапласа.
Імовірність - відношення числа сприятливих випадків до числа можливих. Площа, обмежена ±s - 68%
±2s - 95%
±3s - 99,74%,
тобто 1 бракована деталь на 380 деталей.
Імовірність, що вважається достатньою при оцінці результатів вимірів, називається довірчою, а інтервал, у якому вона знаходиться, - довірчим інтервалом.
Задавшись довірчим інтервалом, розмір записується : Х±3s - це найбільш поширений довірчий інтервал.
Для визначення ймовірності одержання деталей у шуканому інтервалі користуються значенням інтеграла Лапласа, поданого у вигляді таблиці залежності значення інтеграла через розмір Z, виражений у частках s: Z=Х/s
Наприклад: Визначити ймовірність одержання деталей із розмірами від 3 до 4. Х=1мм; z =1/0.71=1.41, за таблицею знаходимо Ф(z)=0.419 або 41.9%
Аналіз точності роботи металорізального верстата
Полягає у виявленні характеру розсіювання розмірів деталей.
На двох верстатах, на яких виготовляють деталі Æ 3мм, були отримані такі розміри: Хі1 2 2 3 5
Хі2 1 2 4 5
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.