Конспект лекцій № 1-27 з дисципліни "Взаємозамінність, стандартизація та технічні вимірювання" (Задачі метрології. Допуски на кутові розміри. Конічні з’еднання), страница 13

Із формули ТА₀ =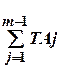=а₁*і₁+а₂*і₂+…а_м-1*і_м-1;

Але а₁=а₂=…=а_м-1=а_ср, тоді ТА₀ =а_ср*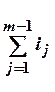; а_ср= ТА_D/.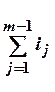

По значенню а_сер  вибирають найближчий квалітет. За відомим квалітетом вибирають допуски розмірів, ураховуючи конструктивно-експлуатаційні вимоги:

 - для охоплюючих - як для основного отвору,

                       - для охоплюваних - для основного вала.

Знаючи допуски складових ланок, визначають Es і Ei для А_D

ES(A₀)=^;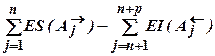

EI(A₀)=^.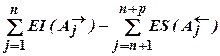

Приклад. Визначити допуски й граничні відхилення розмірів, якщо вихідний розмір А₀= 0,2 ^{+0,25 мм}

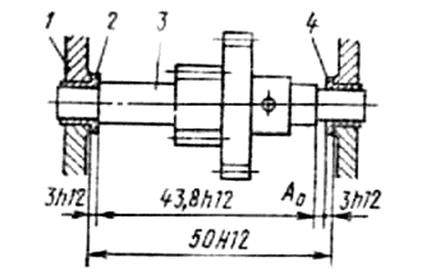
Розв’язок .   Значення і допуск вихідного розміру визначений при проектуванні:

- зазор А₀ необхідний для вільного обертання;             

- повинен запобігати переміщенню;

- не допустити теплового заклинювання.

Спосіб рівних допусків:

Еs(А₀) =250;  Еі(А₀)=0,    число складових ланок : n=1;   p=3; n+p=m-1=5-1=4

Т_сер = 250/ 4=62 мкм. Призначаємо граничні відхилення складових ланок:

          - для охоплюючих - як для основного отвору;

          - для охоплюваних - як для основного валу.

 ES(A₀)=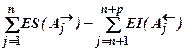 =62-(-186)=248;

EI(A₀)==0-0=0.

Спосіб рівних квалітетів:

1.  Визначаємо  одиниці допусків для розмірів

               А_1,3 ®і _1,3 =1,56 ; А_2,4  ®і _2,4= 0,55

2. Знаходимо число одиниць допуску

а_ср= ТА_D/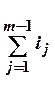=250/2(1,56+0,55)=59,5; відповідає 10 квалітету

9	10	11
40	64	100

За таблицями допусків  назначаємо:

ТА_1,3 = 100 мкм; ТА_2,4 =40 мкм.

3. Перевіряємо рівність сум  допусків:

ТА₀ =(100 +40)2 =280 ® допуск однієї ланки потрібно

зменшити на 30 мкм. Така ланка А₃ ; ТА₃ =70, що приблизно відповідає ТТ9 =62мм

4. Знаходимо граничні відхилення всіх ланок

 А₁ - H10;   А₂, А₄- h10;  A₃ -h9;   ES (A_2,4) =0; EI(A_2,4) =-40

ES(A₁) =100; EI (A₁) =0;                ES (A₃) =0; EI(A₃) =-70;

 Знаходимо граничні відхилення  вихідної ланки:

ES( A₀) =100- (-40 -62-40) =+242;  EI(A₀) =0

Лекція13

Теоретично-імовірнісний метод розрахунку

Метод мінімуму - максимуму допускає можливість сполучення найбільших збільшуючих та найменших зменшуючих  і навпаки.

Будь-яке сполучення дозволяє забезпечити потрібну точність замикаючої ланки, але воно мало ймовірне, оскільки відхилення грунтуються навколо середини поля допуску і такі відхилення зустрічаються переважно.

Якщо припустити дуже малу ймовірність (0,27%) недотримання граничних значень, можна значно розширити допуски складових розмірів і тим самим знизити собівартість, на чому і заснований метод.

Вважаючи, що :

- похибки ланок підпорядковуються закону нормального розподілу;

- межі розсіювання (6d) збігаються з межами полів допусків  ТАj = 6 d_Aj.

При цьому 0,27% виробів замикаючих ланок можуть виходити за межі допуску,оскільки s₀=,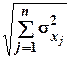

тобто сума середньоквадратичних  відхилень дорівнює квадратному кореню від суми квадратів середньоквадратичних похибок  складових ланок, тоді

ТА₀=.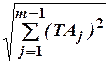

          Ефективність застосування принципів теорії ймовірності при розрахунках допусків розмірних ланцюгів розглянемо на прикладі:

Розмірний ланцюг складається з чотирьох  складальних розмірів, які мають рівні допуски ТА₁=ТА₂=ТА₃=ТА_4.

               За методом мінімумів - максимумів ТА₀=4*ТА_сер;

За імовірнісним методом ТА₀=,

тобто при тій самій точності складових ланцюгів точність замикаючої ланки у другому методі точніше – нам удалося, не витрачаючи додаткових коштів, збільшити точність складання, але при цьому нами заплановано  0,27% браку.

Зворотна задача

Спосіб мінімумів – максимумів.     Виходячи з умови

ТА₀=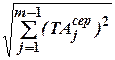, маємо   ТА.

Спосіб імовірнісний. Методика аналогічна способу повної взаємозамінності за винятком:

а_ср= ТА_D/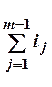  ®   а_ср= ТА_D/.

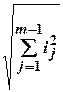Метод групової взаємозамінності

Сутність полягає у тому, що досягнення точності здійснюється шляхом сортування деталей на групи з послідовним складанням вузлів за однойменними групами.