Математические задачи энергетики: Методические указания к выполнению контрольной работы

ВВЕДЕНИЕ

Современное электроснабжение промышленных предприятий, городов и сельскохозяйственных районов представляет собой сложную систему кибернетического типа, отличающиеся большим числом взаимосвязанных элементов и подсистем. Исследование таких систем не представляется возможным без применения достаточно мощного математического аппарата к вычислительной техники.

Все возрастающие темпы электрификации народного хозяйства и энерговооруженности труда приводят к необходимости массового проектирования систем электроснабжения и их развития. Объем этой работы столь велик, что снижение трудозатрат на эту работу становится совершенно необходимым. Это удается решить за счет автоматизации проектирования систем электроснабжения, в свою очередь за счет использования современных математических методов и вычислительной техники.

Народно-хозяйственные затраты на сооружение и эксплуатацию системы электроснабжения большие. Эта обуславливает необходимость принимать в каждом конкретном случае наивыгоднейшее инженерное решение, поскольку многократно повторенная неточность может привести к существенному народно-хозяйственному ущербу. Основой для принятия наилучших решений является математическое исследование операций.

Содержание курса "Математические задачи энергетики" не является изложением всех математических вопросов, необходимых при решении  электроэнергетических задач. Эта дисциплина является лишь "мостиком" между теоретической (чистой) математикой, закладывающей основы математического мышления инженера, и прикладной (инженерной) математикой, служащей аппаратом для решения конкретных технических задач. Такая заблаговременная подготовка студентов позволяет, с одной стороны, разгрузить специальные предметы и сделать их более компактными, а с другой стороны, обеспечить сознательно-критическое применение студентами математики в специальных дисциплинах. 

По курсу предусматривается контрольная работа и экзамен.

Каждый студент должен выполнить контрольную работу, содержание которой приведено ниже. Основой для выбора варианта задания является шифр зачетной книжки и фамилия, имя и отчество студента. Работы выполненные по другим вариантам, не зачитываются.

ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТИ

Определение вероятностей отказа и безотказной работы схемы

электроснабжения

1. Основные понятия

Случайным событием называется всякий факт, который в результате опыта может произойти или не произойти.

Вероятностью события называется численная мера степени объективной возможности этого события. Вероятность события А обозначается Р(А).

Достоверным называется событие U, которое в результате опыта непременно должно произойти.

Р(U) = 1.

Невозможным  называется событие, которое в результате опытане может произойти.

Р(V) = 0.

Вероятность любого события А заключена между нулем и единицей:

0 £ Р(А) £1.

Полной группой событий называется несколько событий, таких, что в результате опыта непременно должно произойти хотя бы одно из них.

Несколько событий в данном опыте называются несовместными, если никакие два из нихне могут появиться вместе.

Несколько событий в данном опыте называются разновозможными, если по условиям симметрии опыта нет оснований считать какое-либо из них более возможным, чем любое другое.

Еслинесколько событий: 1) образуют полную группу; 2) несовместны; 3) равновозможны, то они называются случаями.

2. Теоремы сложения и умножения вероятностей

Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одногоиз событий А или В.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Произведением двух событий А и В называется событие С,состоящее в совместном появлении событияА и события В.

Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Теорема сложения вероятностей

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А+В) = Р(А) + Р(В).

В случае, когда событияА и В совместны,вероятность их сумма выражается формулой

Р(А+В) = Р(А) + Р(В) – Р(АВ),

где АВ - произведение событий А и В.

Теорема сложения вероятностей для нескольких событий

Вероятность суммы нескольких несовместных событий равна сумме их вероятностей:

.

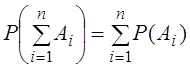В случае, когда событияА_i совместны, вероятность их суммы выражается формулой

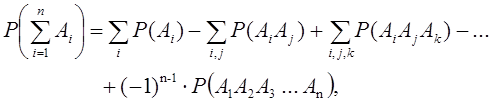
где суммы распространяются на все возможные комбинации различных индексов i, j, k, …, взятых по одному, по два, по три и т.д.

Если событияА₁, А₂, …, А_n несовместны и образуют полную группу, то сумма их вероятностей равна единице:

.

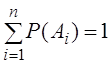Событие  называется противоположным событию А, если оно состоит в непоявлении события А.

Сумма вероятностей противоположныхсобытий равна единице:

.

Условной вероятностью события А при наличии В называется вероятность события, вычисленная при условии, что событие В произошло. Эта вероятность обозначается Р(А/В).

СобытияА и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий

Р(А/В) = Р(А);       Р(В/А) = Р(В).