Математика \ Математические задачи энергетики

Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 6

Таблица 8

Квантили распределения Кохрена G_1-0,05´10²

k	f_j
k	1	2	3	4	5	6	7	8	9	10	¥
2	100	98	94	91	88	85	83	82	80	79	50
3	97	87	80	75	71	68	65	63	62	60	33
4	91	77	68	63	59	56	52	50	49	49	25
5	84	68	60	54	51	48	46	44	42	41	20
6	78	62	53	48	44	42	40	38	37	36	17
7	73	56	48	43	40	37	35	34	33	32	14
8	68	52	44	39	36	34	32	30	29	28	13
9	64	48	40	36	33	31	29	28	27	26	11
10	60	45	37	33	30	28	27	25	24	24	10
20	39	27	22	19	17	16	15	14	14	13	5
60	17	11	9	8	7	6	6	6	5	5	1,7
¥	0	0	0	0	0	0	0	0	0	0	0

Отметим, что наилучшей оценкой k однородных дисперсий служит дисперсия, определяемая как

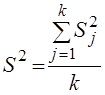
с числом степеней свободы f = kf_j = k(N-1). Эта опенка может использоваться для определения доверительного интервала для s².

t - распределение (t - критерий)

Используется для проверкиоднородности наблюдений, исключения грубых ошибок или выбросов.

Квантили распределенияслучайной величины

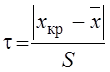зависящего лишь от объема выборки N, по которой определяются и S (х_кр- крайний элемент выборки, наименьший по значению), приведены для р = 0,05 в таблице 9.

Таблица 9

Квантили - распределения при q = 0,05

N	3	4	5	6	7	8	9	10	15	20
t_1-_q	1,41	1,69	1,87	2,0	2,09	2,17	2,24	2,29	2,29	2,62

Все рассмотренные распределения и построенные на их основе критерии предполагают нормальность закона распределения случайной величины. Проверка нормальности при N > 20 осуществляется по критерию А.Н. Колмогорова. При малых выборках могут применяться критерии согласия, основанныена сравнении выборочных ассиметрии и эксцесса сих дисперсиями.

ЗАДАЧА № 3

ЗАДАЧА № 3-1

На основании критерия Стьюдента проверить гипотезу, состоящую в том, что нормально распределенная случайная величина Х имеетМ(Х) = 10 на основании результатов двух испытанийх₁ и х₂.

ЗАДАЧА № 3-2

Пользуясь критерием Пирсона найти с вероятностью р = 0,95 доверительный интервал для s² нормально распределенной случайной величины, если при f, S².

ЗАДАЧА № 3-3

Пользуясь критерием Фишера проверить гипотезу об однородности двух выборочных дисперсий нормально распределенной случайной величины. Результаты опытов: при f₁ и при f₂.

ЗАДАЧА № 3-4

На основания критерий Кохрена проверить гипотезу об однородности выборочных дисперсий ; ; ; ; , каждая из которых определена с вероятностью f, на уровне q = 0,05.

ЗАДАЧА № 3-5

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Скачать файл