Математические задачи энергетики: Методические указания к выполнению контрольной работы, страница 11

Приравнивая х₄ и х₃ ® 0  находим

F(х_i) = 14,0, х₁ = 3,5,       х₂ = 2,5,

х₃ = 0,          х₄ = 0,          х₅ = 1,5,       х₆ = 0,5        (точка Д).

Дальнейшее изменение свободных переменных не приводит к увеличениюF(х), следовательно, точка Д является решением.

3) симплекс–таблица

Необходимо функцию цели и условия ограничений привести к канонической форме.

В задании требуется максимизировать функцию, а канонический вид требует минимизации. Поэтому, умножив функцию цели на (-1), получим:

–f(х_i) = C₀ – (2х₁ +3х₂) ® min.

Для условий, ограничений вводим новые переменные, которые обратят неравенства в равенства

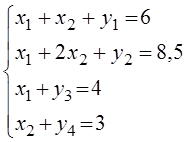
Примем вновь введенные переменныеу₁, у₂, у₃, у₄ в качестве базисных, которые выразим через свободные переменны х₁ и х₂

y₁ = 6 – (х₁ + х₂)

y₂ = 8,5 – (х₁ + 2х₂)

y₃ = 4 – (х₁)

y₄ = 3 – (х₂)

–f(х_i) = 0 –(2х₁ + 3х₂)

Представим уравнения базисных переменных и функции цепи в виде таблицы 17, причем коэффициенты разместим в верхние части клеток.

Таблица 17

Если коэффициенты при свободных переменных в функциицели отрицательны, то полученное решение оптимально, и значения параметров и функции цели определяется столбцом "свободные члены". В противном случае столбец "свободные члены" определяетпервое опорное (базисное) решение при равенстве нулю свободных переменных.

–f(х_i) = 0      [0; 0; 6; 8,5; 4,0; 3,9].

Наибольший коэффициент в функции цели определяет разрешающий столбец (х₂).

Находим наименьшее отношение , которое определяет разрешающую строку. Элемент, стоящий на пресечении разрешающего столбца и разрешающей строки, называют генеральным (обведем его кружком). Разрешающая строка показывает: какая базисная переменная поменяется со свободной переменной х₂ « y₄.

Дляпересчета коэффициентов базисных переменных и функции цели через новые свободные переменные выполним следующее:

1) находим l = 1/а_ij; а_ij - генеральный элемент;

2) все коэффициенты разрешающей строки умножим на l (кроме генерального), а коэффициенты разрешающего столбца - на "-l" изапишем в нижней части клеток;

3) выделим старые значения коэффициентов генеральной строки (e) и новые значения коэффициентов разрешающего столбца (l);

4) числа, вводимые в нижнюю часть клетки на пересечении строки l и столбца S находим перемножением старого значения коэффициентов разрешающей строки и нового значения коэффициентов разрешающего столбца.

После заполнения, всех клеток таблицы осуществляют ее преобразование в новую таблицу:

Таблица 18

Во все верхние отделения клеток разрешающей строки и разрешающего столбца заполняются числа из нижних отделений предыдущей таблицы; в остальные клетки помешают алгебраическую сумму чисел данной клетки.